















Физический и геометрический смысл производной в ЕГЭ
Физический и геометрический смысл производной в ЕГЭ — Какие задачи встречаются в задании 8 ЕГЭ по математике?
Задание 8 включает в себя задачи на понимание смысла производной как величины, характеризующей скорость изменения функции; задачи на геометрический и физический смысл производной; задачи, связанные с первообразной и её геометрическим смыслом.
Физический и геометрический смысл производной в ЕГЭ, задание 8 ЕГЭ по математике – проблема определения производной
Безусловно, самым наглядным из корректных определений производной есть определение ее через предел приращения функции к приращению аргумента. При этом многие ученики 11-го класса не проходят в школе тему пределов, которые ни в каком виде не включены в программу ЕГЭ. И чтобы научиться решать задачи ЕГЭ, лучше всего изучить понятие производной «на пальцах».
Мы живем в динамическом, постоянно изменяющемся мире. Постоянно меняется вокруг всё в любой из областей жизни: температура в области физики, стоимость валюты в экономике, популяция вида в области биологии, соотношение веществ в химических реакциях и так далее (здесь можно упомянуть любые подобные изменения на своё усмотрение). Помимо значения величины также важно то, насколько эта величина быстро меняется. Для специалистов самых разных областей скорость изменения величины может быть не менее информативной, чем само значение величины. Так как математика занимается тем, что описывает реальный мир, так сказать, на бумаге, в математике вводится специальное понятие, описывающее скорость изменения величины, и называется оно — производная.
Итак, производная — это скорость изменения. Производная чего-либо показывает, насколько быстро и в какую сторону меняется это что-либо.
Вводим определение производной. Давайте представим себе какую-то функцию – просто выберем и нарисуем любую произвольную. Как же именно задается производная? Как уже было сказано, производная — это скорость изменения. Но, очевидно, для этой, нарисованной нами функции, скорость изменения везде разная: посмотрите, где-то функция растет быстрее, где-то медленнее, а где-то вообще убывает, то есть — меняется с разной скоростью. Выходит, здесь в разных точках производная функции — разная.
Поэтому рассмотрим какую-то отдельную точку х0. В этой точке функция имеет значение f(х0). Давайте теперь к х0 прибавим некоторое маленькое-маленькое значение ∆х и перейдем в новую точку х1, которой соответствует f(х1). Пусть разница между f(х1) и f(х0) будет ∆y.
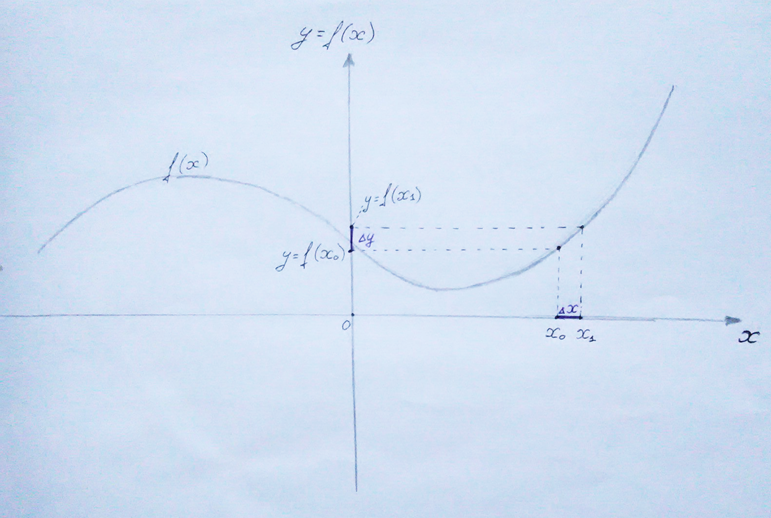
Итак, производная — это ∆y/∆х, если брать ∆х очень маленьким. Почему очень маленьким? Давайте обозначим х2 подальше от х1 и, соответственно, f(х2), видим два получившихся треугольника. Это два прямоугольных треугольника с разными углами — поэтому они не подобны, то есть не являются копией друг друга в увеличенном/уменьшенном виде. Если бы они были подобны, тогда значение ∆y/∆х было бы одинаковым для обоих треугольников, но у наших треугольников это значение разное. Вот для чего говорились слова «очень маленькое значение ∆х». Штука в том, что, чем меньшее значение ∆х мы возьмем, тем более «точное» значение производной получим.
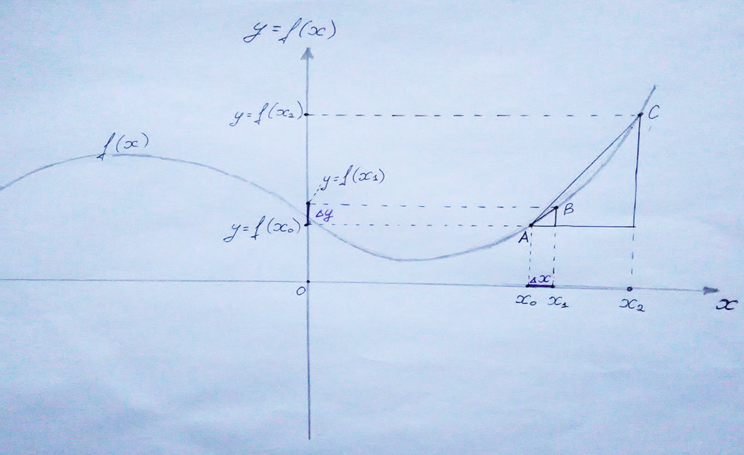
А как получить совсем точное значение производной? Ведь мы всегда можем взять еще меньшее, и еще меньшее значение ∆х. Давайте понаблюдаем, что будет происходить, если мы будем бесконечно приближать точки А и В.
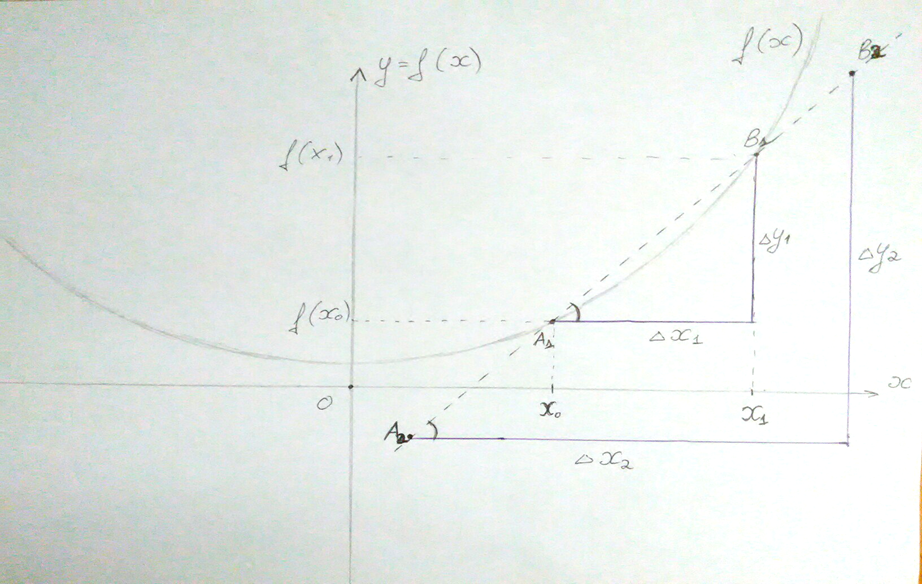
Нарисуем еще один рисунок. Здесь так же есть некоторая функция, выбранная точка х0 и точка х1, которым на функции соответствуют точки А1 и В1. Давайте соединим точки А1 и В1 прямой (назовем ее прямая m), продолжим ее и на продолжениях отметим еще точки А2 и В2. Эти два получившихся треугольника (см. рисунок ниже) прямоугольны и имеют одинаковые углы, то есть они подобны, и в данном случае отношение ∆y/∆х одинаково: ∆y1/∆ =∆y2/∆х2. То есть, где бы на прямой мы не выбрали две точки, отношение ∆y/∆х будет постоянным.
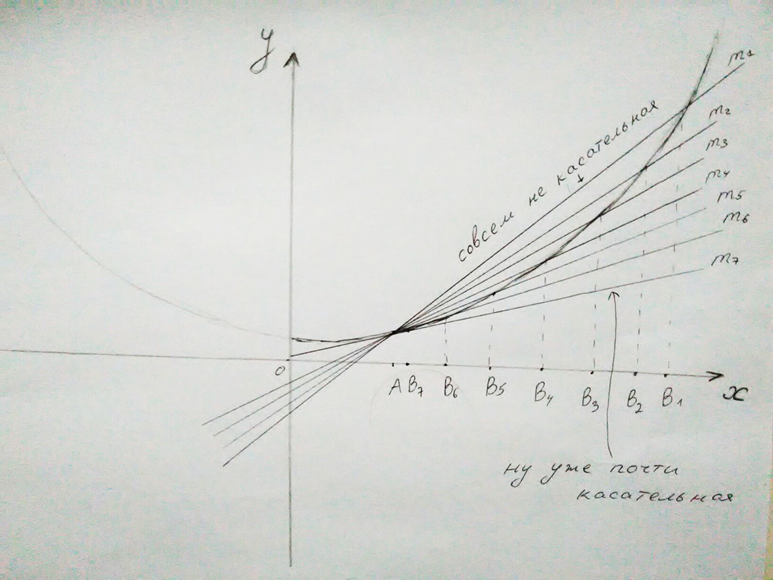
Начнем теперь приближать точку В к точке А1, обозначим точки В1, В2… В7
и проведя через них прямые m1…m7. Посмотрите внимательно на эти прямые. Чем ближе точка В к точке А, тем больше прямая между ними напоминает… касательную! Помните, мы раньше пришли к выводу о том, что чем меньше ∆х, тем ближе отношение ∆y/∆х к значению производной? Смотрите, что получается: чем меньше мы возьмем ∆х, тем ближе прямая m к тому, чтобы быть касательной, а чем меньше ∆х, тем лучше. Поэтому идеально точно производную мы находим так.




- Как поступить в любой вуз по олимпиаде в 2026 году.
- Бесплатный курс ЕГЭ по математике 2026 (профиль)
- Бесплатный курс ЕГЭ по русскому языку 2026
- Бесплатный курс ОГЭ по математике 2026
- 10 главных правил: Как сдать ЕГЭ на 80+ баллов


Физический и геометрический смысл производной — Разбор задания 8 ЕГЭ по математике
Если вам дан график функции и вам нужно в какой-то точке х0 найти производную, нужно действовать следующим образом:
- Проведите касательную к функции в этой точке.
- На касательной выберите 2 точки (любые, какие удобней).
- Найдите разницу между этими точками по вертикали и по горизонтали и первую делим на вторую. Полученное число и есть производная в точке х0. Обозначается она f`=(x0)
Отрабатывать этот алгоритм стоит уже на конкретных примерах, так как, наверняка, ваша голова уже забита теорией, и чем раньше начнется практика на конкретных заданиях, тем лучше.
Физический и геометрический смысл производной — Прототипы 8 задания ЕГЭ по математике
Задание 1
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.

Ответ: 2
Задание 2
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
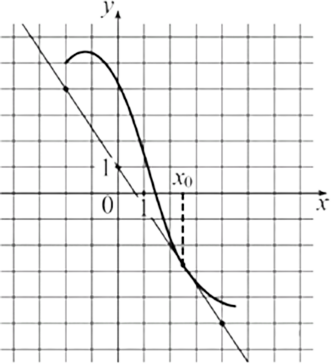
Ответ: -1,5
Задание 3
На рисунке изображены график функции y=f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f(x) в точке x0.
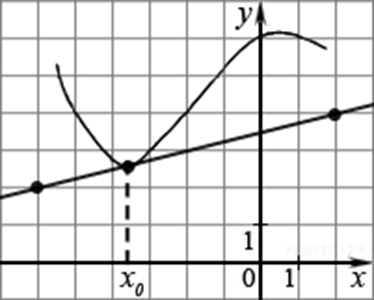
Ответ: 0,25
Ответы на часто задаваемые вопросы

Наибольшее и наименьшее значение функций — Что нужно делать в задании 12 ЕГЭ по профильной математике? Задание 12 ЕГЭ по профильной математике — это нахождение точек максимума и минимума функции,…

Тригонометрия — Что нужно делать в задании 13 ЕГЭ по профильной математике? Задание 13 ЕГЭ по профильной математике – тригонометрия. Необходимо разбираться в основных понятиях тригонометрии: синус, косинус, тангенс, котангенс…
