8bit > Математика ЕГЭ > Задачи на сплавы и смеси – ЕГЭ по математике

Задачи на сплавы и смеси – ЕГЭ по математике

30-05-2023

Дополнительные темы

Краткий ответ, как решать задачи на сплавы и смеси

В условиях задач на процентные доли в смесях смешиваются растворы (сплавы) с разными массами и концентрациями некоторого вещества, формируя раствор общей массы и новой концентрации. Какая-то из величин (масса какого-то из растворов, или процент содержания вещества) является искомой.

Задачи на сплавы и смеси ЕГЭ математика– основные формулы

Прежде чем зазубривать две формулы для решения задач на сплавы и смеси из ЕГЭ, надежнее будет понять, почему эти формулы справедливы.

Во-первых, при смешивании растворов (сплавов) сохраняется масса (объем).

То есть, сумма начальных масс (объемов) равна массе конечной смеси:

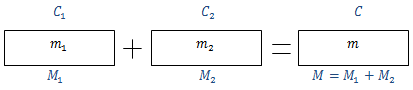
Задачи на сплавы и смеси ЕГЭ

m₁ + m₂ = m — формула достаточно тривиальная, но иногда про нее попросту забывают.

И второе. Концентрация — это масса (объем) вещества, деленная на общую массу раствора.

$С=\frac{m_{вещества}}{M_{общая}}$

Задачи на смеси ЕГЭ математика: прототипы

Задание 1

Смешали 4 литра 15-процентного водного раствора некоторого вещества с 6 литрами 25% водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Ответ: 21

Задание 2

В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора?

Ответ: 5

Задание 3

Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 19-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Ответ: 17

Задачи на сплавы ЕГЭ математика: прототипы

Задание 4

Имеется два сплава. Первый сплав содержит 10% никеля, второй — 30% никеля.

Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля.

На сколько килограммов масса первого сплава меньше массы второго?

Ответ: 100

Подготовьтесь к ЕГЭ или ОГЭ за 4 месяца

Интенсивный онлайн курс в Годографе с экспертами МЦКО

Узнать подробнее

Ответы на часто задаваемые вопросы

Основные формулы для решения задач на проценты, смеси и сплавы

m1 + m2 = m — формула достаточно тривиальная, но иногда про нее попросту забывают. Концентрация — это масса (объем) вещества, деленная на общую массу раствора.

Как выглядит решение задач на проценты, смеси и сплавы?

Возьмем следующий пример: В сосуд, содержащий 5 литров 12-процентного водного раствора некоторого вещества, добавили 7 литров воды. Сколько процентов составляет концентрация получившегося раствора? Для начала вычислим, сколько вещества содержится в 12% растворе. Для этого 12% умножаем на 5 литров раствора: 0,12*5=0,6 л. Далее определим объем нового раствора: 5+7=12 л. Поскольку в чистой воде вещества нет, то в новом растворе количество не изменилось – 0,6 л. Вычисляем концентрацию получившегося раствора: 0,6/12*100%=5%. Ответ: 5.

Что такое концентрация вещества в задачах на смеси и сплавы?

Концентрация — это масса (объем) вещества, деленная на общую массу раствора.

Все статьи