Что такое теория вероятности в ЕГЭ по математике?

Теория вероятности – это раздел математики, изучающий случайные события и величины, а также их свойства и различные арифметические операции над ними. Вероятность показывает количественную оценку возможности наступления некоторого события.

Классическое определение вероятности

По сути, все задачи первой группы из ЕГЭ по теории вероятности являются чем-то вроде: «В ящике лежит 4 шара, один из них черный. Какова вероятность с первого раза случайно вытащить черный шар?». То есть вероятность события есть отношение благоприятного числа исходов к общему числу исходов.

Посмотрим, как решаются задания 1–11 из практикума.

В 4 номере число благоприятных исходов подсчитывается перебором, а случаи 3–5 и 5–3 (кол-во очков на костях) — исходы разные, и считать их нужно отдельно. Общее же число исходов быстрее посчитать не перебором, а 6*6 — на каждый из 6 вариантов на первой кости приходится по 6 вариантов на второй. Вещи это довольно простые, но обсудить их хотя бы один раз стоит.

Приступая к другой задаче, стоит иметь в виду, что иногда условие задачи можно переформулировать более наглядным для себя образом, если суть происходящего не меняется. Эту же самую задачу можно представить так:

«Пусть за круглый стол с 9 стульями садятся 2 девочки. Мальчиков нет вообще. Сначала заходит одна девочка и садится на произвольное место. Потом заходит вторая и садится на произвольное место из свободных. Какова вероятность, что она сядет рядом?».

При такой формулировке любой ученик сможет посчитать, что осталось свободных 8 мест, только 2 из них подходящие — рядом с первой девочкой, и разделить 2 на 8.

Были ли мальчики, или нет, заходили девочки одновременно, или по очереди, и если по очереди, то место, куда села первая девочка — это всё не имеет значения. Важно лишь то, что было 9 мест и 2 девочки. Иногда такой подход, подобное «переформулирование» задачи заметно упрощает процесс умозрительного представления и решения.

Достаточно распространен немного более усложненный вариант этой же задачи. «Есть 4 комнаты по 4 стула в каждой, 16 человек рассаживают по стульям, какова вероятность двум близнецам оказаться в одной комнате?» Аналогично, представляем, что человек не 16, а всего 2 — наши близнецы, и мы запускаем их по очереди. Первый садится куда-то, куда — не важно. Важно то, что, когда второй пойдет садиться на какой-то стул, «подходящих» стульев будет 3 (в комнате с первым близнецом), а всего свободных — 15.

Теория вероятности в ЕГЭ — «Хотя бы один из»

Номер 4 и 5 — задача, в которой надо найти вероятность того, что «хотя бы одно из…» Задачи с такой постановкой условия решаются двумя способами:

1. Решение с помощью формулы теоремы 2, решение «в лоб» – оправдывает себя только в случае двух событий.
2. Решение через противоположное событие – незаменимо в случае трех и более событий; не подходит, если события несовместны или зависимы.

Давайте пойдем методом от противного и возьмем обратное утверждение к «хотя бы одна лампа не перегорит». Неправильно – «хотя бы одна лампа перегорит», но правильно – «перегорят все». То есть перегорит первая, и вторая, и третья, если бы она была по условию задачи — а это уже произведение событий, притом обратных.

Итак, P (A + B + C) = 1 – P (Ā * Ḃ * Ć)  — формула, справедливая для любого (можно и больше трех) числа событий. Не обязательно знать формулу, важно понимать сам принцип, который формула отображает.

На примере номера 16 разбираем оба способа решения. Оба способа очень важны, так как в случае несовместных или зависимых событий второй способ не действителен.

Онлайн подготовка к ЕГЭ и ОГЭ 2025 с выгодой до 30%

Занятия в мини-группах с экспертами ЕГЭ по всем школьным предметам

Узнать подробнее

Теория вероятности в ЕГЭ решение задач: теоремы о вероятностях

Введем немного терминологии:

• События независимы, если наступление одного их них не изменяет вероятность наступления другого. Интуитивно знакомое понятие и без математической строгости.
• События совместны, если (здесь скажем простым языком) они могут произойти оба, одновременно. Например, падение двух монет орлом вверх — совместные события. Но падение одной монеты орлом вверх и орлом вниз — события, очевидно, несовместные.

События называются противоположными, если они несовместны и сумма их вероятностей равна 1. Простым языком: если событие А — «кое-что произошло», то  Ā — то же самое не произошло. P (Ā) = 1 – P (A).

Произведением событий А и В называется событие АВ, заключающееся в том, что произошли оба события одновременно: и А, и В.

То есть, вероятность произведения есть произведение вероятностей.

Суммой событий А и В называется событие А+В, заключающееся в том, что произошло хотя бы одно из событий А и В.

Для несовместных событий, очевидно, P (AB) = 0. Случаи, когда события совместны, но зависимы, бывают в задании 4 крайне редко, и в подобных номерах недостающая информация, как правило, известна из условия.

За исключением еще одного момента, это, в принципе, вся теория, которую необходимо знать, но её надо знать четко, так как она требуется в каждой второй задаче задания 4.

Теория вероятности в ЕГЭ  – дерево событий

Рассмотрим на примере. Случайно выбранное стекло (на рынке) может оказаться продукцией первой фабрики (45%), или второй (55%) с определенной вероятностью быть бракованным в первом и во втором случае. Условие можно представить в виде схемы («дерева»), включающей в себя все возможные исходы.

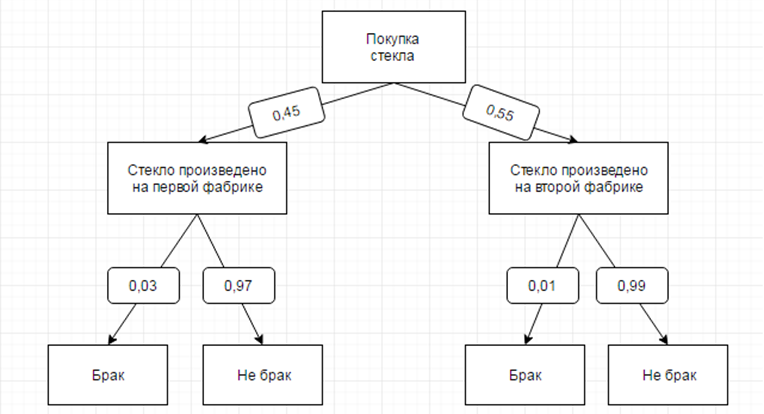
Нарисовав такую схему, легко считать конечные вероятности. Если спрашивается вероятность того, что случайно купленное стекло окажется бракованным, то нам «подходят» два конечных исхода:

1. Стекло произведено на первой фабрике и браковано, вероятность такого исхода 0,45 * 0,03 = 0,0135;
2. Стекло произведено на второй фабрике и браковано, вероятность 0,55 * 0,01 = 0,0055.

Значит, стекло окажется бракованным с вероятностью 0,019.

События «случайное стекло произведено на первой фабрике» и «случайное стекло, произведенное на первой фабрике, браковано» — совместны и независимы, поэтому их вероятности мы перемножили для того, чтобы найти вероятность события «стекло будет произведено на первой фабрике и окажется бракованным». А вот конечные исходы мы просто сложили, так как события, очевидно, несовместны (стекло произведено только на какой-то одной фабрике) и подходят нам оба, т.е. случай «хотя бы один из».

Важные уточнения к решению задач ЕГЭ на теорию вероятности

Во-первых, метод хорошо работает и в случае постановки условия «наоборот», когда, скажем, была бы известна вероятность приобрести в магазине бракованное стекло, но не было бы известно, как много производят первая и вторая фабрика (в процентном соотношении). Тогда вместо 45% и 55% на нашей схеме были бы неизвестные  и , через которые мы бы выразили известную вероятность брака случайного стекла.

Во-вторых, к подобной задаче можно рисовать, как правило, не одну блок-схему. Ниже приведен пример того, как иначе, неправильно, можно было бы изобразить условие номера 27.

В этом варианте, казалось бы, тоже перебраны все конечные исходы, но для такой блок-схемы у нас нет данных: условие сформулировано таким образом, что вероятности мы можем выписать именно для первой блок-схемы.

Иногда не совсем очевидно, как именно рисовать блок-схему, поэтому вот вам универсальный совет: если вы нарисовали схему и видите, что ваше условие, ваши вероятности к ней не подходят — просто нарисуйте ее иным способом. Существует как минимум два способа изображения условия.

Теория вероятности в ЕГЭ — Примеры задач и решения 

Теория вероятности ЕГЭ задания 4 и 5 можно условно разделить на 2 группы:

1. Задачи, базирующиеся на самом определении вероятности;
2. Задачи, требующие знаний об операциях сложения и умножения вероятностей.

Классическое определение вероятности

Теоремы на сложение и умножение вероятностей