Коротко о том, что такое логарифмические уравнения в ЕГЭ

Уравнение, содержащее неизвестное под знаком логарифма или (и) в его основании, называется логарифмическим уравнением. Логарифм — это степень. Более половины простейших логарифмических уравнений и заданий с логарифмами в ЕГЭ решаются логически с помощью одного лишь определения логарифма, поэтому его надо знать идеально.

Логарифмические уравнения в ЕГЭ  – базовые знания о логарифмах

Итак, наверное, каждый уже решал уравнения типа 2^x = 8, где в обеих частях уравнения получаем одинаковые основания и приравниваем степени. Но что делать, если получить одинаковые основания с удобными степенями нельзя, как, например, если 2^x = 7 или 2^x = 11? Ведь уравнения, описывающие реальный мир, совершенно не обязательно будут иметь красивые и удобные решения. Хотелось бы иметь возможность как-то выразить решение такого уравнения, такое число, математическим языком.

Как это сделать? С помощью следующей записи: допустим, если 2^x = 7, то пишут, что x=log₂7 ― эта запись дословно означает, что икс равен степени, в которую нужно возвести 2, чтобы получить 7. Называется эта штука логарифмом, и произносят такую запись следующим образом: логарифм семи по основанию двух. Соответственно, если 3^x = 5, то x=log₃5 ― икс равен степени, в которую нужно возвести 3, чтобы получить 5.

Переходим к общему случаю: если у нас есть уравнение a^x = b, то икс будет равен:

x=log_ab

В силу ограничений показательной функции, в которой для нашего примера a>0, b>0, у логарифма сохраняются такие же ограничения: основание логарифма а и аргумент логарифма b должны быть положительны! Но логарифм более коварный, у него появляется одно дополнительное ограничение a≠1.

Логарифм — всего лишь обозначение. Это не новый объект, как синус или производная, а просто новое обозначение. Представьте, что нам нужно найти сумму степени, в которую надо возвести 10, чтобы получить 8, и степени, в которую надо возвести 10, чтобы получить 125. Представить это в голове достаточно сложно, но с помощью логарифмов это решается очень просто, в два действия. Немного практики – и вы этому научитесь.

Онлайн подготовка к ЕГЭ и ОГЭ 2025 с выгодой до 30%

Занятия в мини-группах с экспертами ЕГЭ по всем школьным предметам

Узнать подробнее

Логарифмические уравнения в ЕГЭ по математике, решение

Приступим к следующей серии примеров. Итак, у нас есть log_a b – степень, в которую надо возвести a, чтобы получить b. То есть если возвести a в степень log_a b, получим, что:

Данная формула называется основным логарифмическим тождеством.

Логарифмические уравнения в ЕГЭ по математике – как складывать логарифмы

Возьмем в качестве примера логарифм log₂4 + log₂8. Первое слагаемое равно 2, второе – 3, сумма равна 5. При этом 5 можно представить как логарифм 32 по основанию 2. Выходит, log₂4 + log₂8 = 5 = log₂32.

Как связаны 4, 8 и 32? Если умножить 4 на 8, получается 32. Выходит, если сложить два логарифма с одинаковым основанием, получается логарифм того же основания от выражения, равного произведению чисел под начальными логарифмами:

В общем виде:

Помнишь, что происходит со степенями при перемножении чисел с одинаковыми основаниями? Они складываются. Логарифм — это степень, и, как видишь, здесь сложение степеней происходит также в случае перемножения чисел.

Аналогично с формулой разности логарифмов:

Как мы уже выяснили, складывая два логарифма, мы получаем логарифм произведения. Давай сложим два одинаковых логарифма:

Если мы сложим, скажем, 5 одинаковых логарифмов, то

Получаем, что, складывая n одинаковых логарифмов, будет

И последнее, что следует запомнить для решения логарифмических уравнений на профильный уровень ЕГЭ, – это формулу перехода к новому основанию:

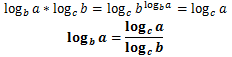
И его частный случай: