8bit > Математика ЕГЭ > Квадратные уравнения в ЕГЭ

Квадратные уравнения в ЕГЭ

22-05-2023

Дополнительные темы

Демоверсия ЕГЭ по математике 2024 года профиль и база Задачи на сплавы и смеси в ЕГЭ по математике Физический и геометрический смысл производной в ЕГЭ Арифметическая прогрессия в ЕГЭ Задачи прикладного характера в ЕГЭ по математике 8 задание ЕГЭ по математике Действия со степенями в ЕГЭ по математике Адиабатический процесс в ЕГЭ по математике Геометрическая и арифметическая прогрессия в ЕГЭ по математике Задачи прикладного содержания в ЕГЭ по математике Показательные уравнения в ЕГЭ Логарифмические уравнения в ЕГЭ по математика Кубические уравнения в ЕГЭ Квадратные уравнения в ЕГЭ Линейные уравнения в ЕГЭ по математике Теория вероятности в ЕГЭ по математике Задания на теорию вероятности в ЕГЭ Теория вероятности в ЕГЭ Стереометрия в ЕГЭ Планиметрия в ЕГЭ по математике, разбор задания 1 Изменения в ЕГЭ по математике в 2024 году Как подготовиться к ЕГЭ по математике 2024 года Задачи прикладного характера в ЕГЭ по математике Неравенства в ЕГЭ Стереометрия в ЕГЭ – теория и практика Тригонометрия в ЕГЭ Наибольшее и наименьшее значение функций в ЕГЭ Структура ЕГЭ по математике в 2023 году Производная и первообразная в ЕГЭ Вычисления и преобразования в ЕГЭ Простейшие уравнения в ЕГЭ

Как решаются квадратные уравнения в ЕГЭ?

Квадратные уравнения – это уравнения вида ax² + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член. Они решаются через нахождение дискриминанта или по теореме Виета.

Квадратные уравнений в ЕГЭ по математике, формулы

Как сделать вывод решения квадратного уравнения? Для этого в квадратном уравнении выделяем полный квадрат, берем корень от обеих частей и выражаем неизвестную.

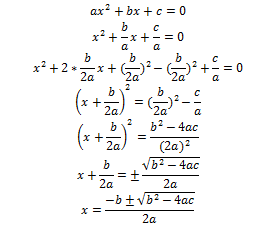
квадратных уравнений ЕГЭ профиль

Нам также пригодится формула: D₁ = k² – ac, где k = b/2 (используется только для четного коэффициента b). Тогда корни уравнения будут находиться по формуле:

$x_{1,2}=\frac{-k\pm \sqrt{D_{1}}}{a}$

Данная формула может позволить уменьшать расчеты как минимум в трех заданиях с квадратными уравнениями в ЕГЭ.

Решение квадратных уравнений – это не магия

Ребята, слабые в математике, часто жалуются на то, что для них математика – это «магия», и в школах просто забивают головы алгоритмами решения без пояснений, почему алгоритмы такие, откуда формулы берутся, и что вообще мы решаем. Это не способствует изучению предмета, но за короткий промежуток подготовки невозможно получить полноценное правильное представление о математике и научиться решать все, что есть на экзамене ЕГЭ.

Соответственно, если сначала решение квадратного уравнения дается как неоспоримую истину, то к концу курса обучения при наличии свободного времени для подготовки, эти неприятные моменты можно будет исправить. Однако имей в виду: один год – не так много, как может показаться.

К концу курса подготовки к ЕГЭ никакой «магии» остаться не должно. Поэтому стоит стараться вникать во все мелочи. Например, откуда берется формула для решения квадратного уравнения. Почему это важно? Как только ты с легкостью будешь решать задания 1–11 и перейдешь к заданиям 12–18 — тут все подобные отступления, казавшиеся «лишними», сыграют немалую роль.

Онлайн подготовка к ЕГЭ и ОГЭ 2025 с выгодой до 30%

Занятия в мини-группах с экспертами ЕГЭ по всем школьным предметам

Узнать подробнее

Теорема Виета для решения квадратных уравнений в ЕГЭ

Теперь рассмотрим теорему о том, что квадратный многочлен, имеющий 2 решения в нуле, разбивается на множители: a (x – x₁) * (x – x₂). Но для начала стоит напомнить и показать справедливость теоремы Виета.

Допустим, у нас есть квадратное уравнение с одним из корней x = 3. Тогда, подставив x = 3, мы получим ноль. А в каком еще случае мы будем получать ноль в любом уравнении при подстановке x = 3? Мы тоже будем получать ноль, если у нас в уравнении есть множитель x–3. Тогда при x = 3 всё уравнение станет равно нулю.

А не значит ли это, что квадратное уравнение, которое при x = 3 обращается в ноль, можно преобразовать, «выделив» из него множитель x – 3? Если это предположение верно, оно должно работать для обоих корней, то есть тогда можно выделить множители x – x₁ и x – x₂. Если мы просто перемножим их, то получим x², а не ax², как в квадратном уравнении общего вида. Поэтому давайте попробуем, перемножив их, умножить еще на a: a(x – x₁)(x – x₂) — и это должно быть равно ax² + bx + c. Раскрываем скобки, делим все на a – и вуаля – знакомая нам теорема Виета.