8bit > Математика ОГЭ > Практико-ориентированные задачи ОГЭ по математике

Практико-ориентированные задачи ОГЭ по математике

22-05-2023

Дополнительные темы

Демоверсия ОГЭ по математике 2024 года 16 задание ОГЭ по математике – окружность, круг и их элементы 15 задание ОГЭ по математике – треугольники Практико-ориентированные задачи ОГЭ по математике 14 задание ОГЭ по математике Теория вероятностей в ОГЭ по математике 9 класс 21 задание ОГЭ по математике 20 задание ОГЭ по математике 12 задание ОГЭ по математике – расчеты по формулам Функции арифметического квадратного корня — ОГЭ по математике 11 задание ОГЭ по математике 13 задание ОГЭ по математике Рациональные уравнения ОГЭ 9 задание ОГЭ по математике 7 и 8 задания ОГЭ по математике 6 задание ОГЭ по математике Демоверсия ОГЭ по математике 2023 года

Что такое практико ориентированные задачи в ОГЭ?

Это пласт задач, которые моделируют жизненные ситуации. Для их решения нужно изучить схему и вдумчиво прочитать пару абзацев текста. Вспомним основные понятия, теоремы и формулы, которые пригодятся при решении практико-ориентированных задач по математике ОГЭ 2024.

Элементы треугольника – основные определения

Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к противоположной стороне или к ее продолжению (в случае тупоугольных треугольников).

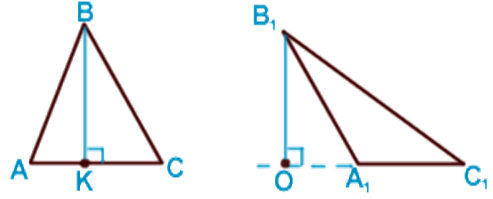
треугольник огэ математика

В любом треугольнике можно провести три высоты.

Высоты треугольника или их продолжения пересекаются в одной точке.

В остроугольном треугольнике точка пересечения высот находится внутри области треугольника.

В тупоугольном треугольнике точка пересечения прямых, содержащих высоты, находится вне области треугольника.

В прямоугольном треугольнике катеты являются высотами.

Медианой треугольника называется отрезок, соединяющий вершину треугольника с серединой противоположной стороны. В треугольнике можно провести три медианы.

Медианы треугольника пересекаются в одной точке. Обычно эту точку называют центром треугольника, или центром масс.

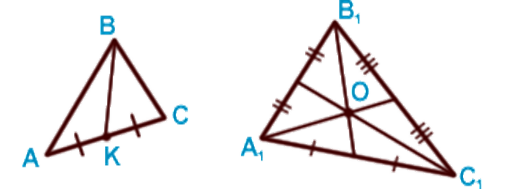
треугольник огэ математика

Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.

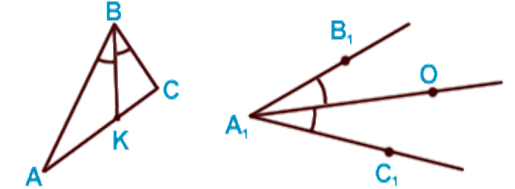
биссектриса огэ математика

Обратите внимание, что биссектриса угла — это луч, делящий угол на два равных, а биссектриса треугольника — это отрезок, часть луча, ограниченная стороной треугольника. В любом треугольнике биссектрисы пересекаются в одной точке, являющейся центром вписанной окружности.

Признаки равенства треугольников – подготовка к ОГЭ, практико ориентированные задачи

Треугольники называются равными, если их можно совместить наложением.

В геометрии используются три признака равенства треугольников.

Первый признак равенства треугольников (по двум сторонам и углу между ними).

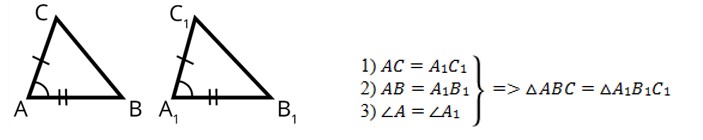
равенства треугольников огэ математика

Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.

Второй признак равенства треугольников (по стороне и двум прилежащим к ней углам).

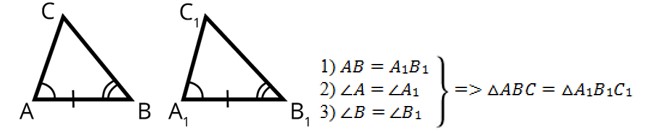
равенства треугольников огэ математика

Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.

Третий признак равенства треугольников (по трем сторонам).

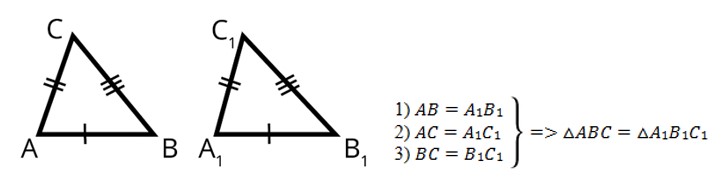
равенства треугольников огэ математика

Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.

Подобные треугольники – практико-ориентированные задачи из ОГЭ

Будем рассматривать следующие два треугольника:

Определение 1

Два треугольника называются подобными, если углы все углы одного треугольника соответственно равны углам другого и треугольника, и все сходственные стороны этих треугольников пропорциональны, то есть:

Обозначение: ABC ∼ A₁ B₁ C₁

Определение 2

Число k, равное отношению сходственных сторон подобных фигур называется коэффициентом подобия этих фигур.

Признаки подобия треугольников

Приведем формулировки трех признаков подобия треугольников.

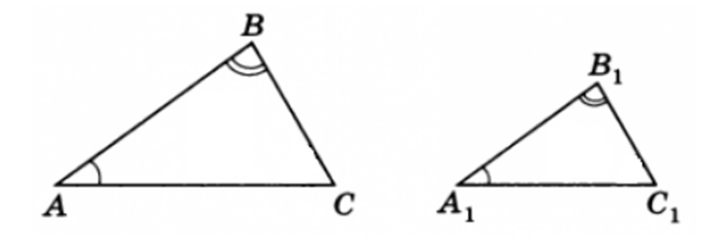
Первый признак подобия треугольников: Если два угла одного треугольника соответственно равны двум углам второго треугольника, то такие треугольники подобны.

То есть, если

то треугольники ABC и A₁ B₁ C₁ подобны.

треугольник огэ математика

Второй признак равенства треугольников: Если две стороны одного треугольника пропорциональны соответствующим сторонам второго треугольника и углы между этими сторонами равны, то данные треугольники подобны.

То есть, если

то треугольники ABC и A₁ B₁ C₁ подобны.

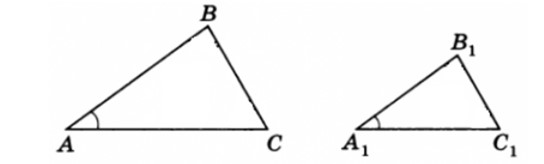
треугольник огэ математика

Третий признак подобия треугольников: Если три стороны одного треугольника пропорциональны трем соответствующим сторонам второго треугольника, то такие треугольники подобны.

То есть, если

то треугольники ABC и A₁ B₁ C₁ подобны.

Соотношение площадей подобных треугольников

С этим понятием связана следующая теорема о соотношении площадей подобных треугольников. Рассмотрим её без доказательства.

Теорема 1

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия сторон, то есть

$\frac{S_{ABC}}{S_{A_{1}A_{2}A_{3}}}=k^{2}$

Средняя линия треугольника – практико-ориентированные задачи по математике ОГЭ 2024

Средняя линия треугольника — это отрезок, соединяющий середины двух его сторон. На рисунке средние линии:

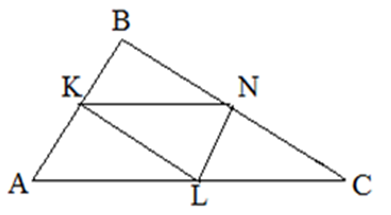
Средняя линия треугольника огэ математика

Свойства средней линии треугольника

Средняя линия треугольника параллельна одной стороне и равна ее половине. Например, на рисунке:

В любом треугольнике три средних линии, при пересечении которых образуются 4 равных треугольника, подобных исходному с коэффициентом 1/2.
Средняя линия отсекает треугольник, который подобен данному, а его площадь равна площади исходного треугольника.

Средняя линия трапеции:

$MN=\frac{1}{2}(a+b)$

где a, b — основания трапеции.

Прямоугольный треугольник

Треугольник называется прямоугольным, если у него один угол прямой. Сторона, противолежащая прямому углу, называется гипотенузой, две другие стороны — катетами.

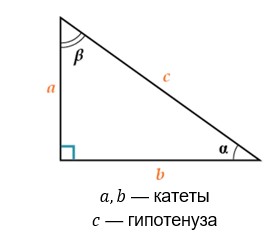
огэ математика

В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.

Теорема Пифагора:

c²=a²+b²

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

Признаки равенства прямоугольных треугольников:

Признаки равенства прямоугольных треугольников

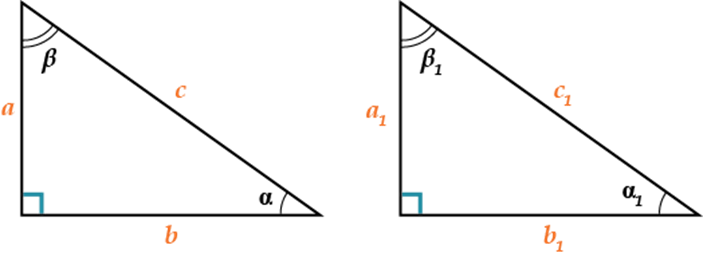
По двум катетам: a=a₁,b=b₁
По катету и гипотенузе: a=a₁,c=c₁или b=b_1,c=c₁
По катету и прилежащему острому углу:

По катету и противолежащему острому углу:

По гипотенузе и острому углу:

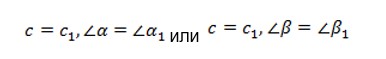
Теорема Пифагора огэ математика

Признаки подобия прямоугольных треугольников:

По одному острому углу:

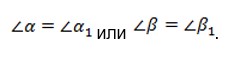
огэ математика

Из пропорциональности двух катетов:

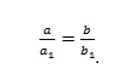
огэ математика

Из пропорциональности катета и гипотенузы:

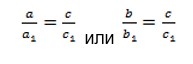
огэ математика

Площадь прямоугольного треугольника:

Через катеты:

$S=\frac{1}{2}ab$

Площадь квадрата, прямоугольника, треугольника

Площадь квадрата:

Площадь квадрата равна квадрату длины его стороны: S=a ².

Площадь квадрата равна половине квадрата длины его диагонали:

$S=\frac{1}{2}d^{2}$

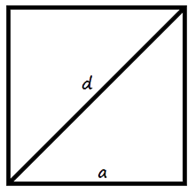
Площадь квадрата огэ математика

Площадь прямоугольника:

Площадь прямоугольника огэ

Площадь прямоугольника равна произведению длин двух его смежных сторон: S=a*b

Площадь треугольника:

Площадь треугольника равна половине произведения длины стороны треугольника на длину проведенной к этой стороне высоты:

$S=\frac{1}{2}ah$

Разбор практико-ориентированных задач ОГЭ 2024

Рассмотрим пример из экзамена:

Разбор практико-ориентированных задач ОГЭ 2023

Прочитайте внимательно текст и выполните задания 1–5.

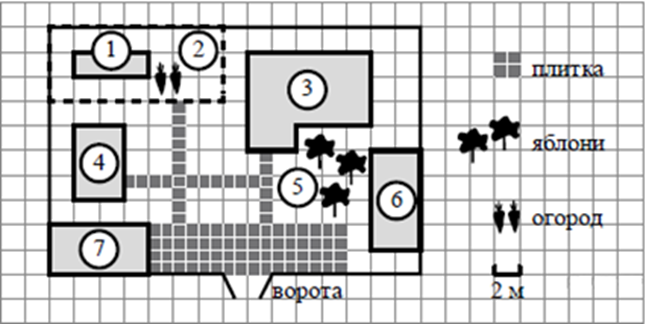
На плане изображено домохозяйство по адресу: с. Авдеево, 3-й Поперечный пер., д. 13 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Выезд и въезд осуществляются через единственные ворота.

При входе на участок справа от ворот находится баня, а слева — гараж, отмеченный на плане цифрой 7. Площадь, занятая гаражом, равна 32 кв. м.

Жилой дом находится в глубине территории. Помимо гаража, жилого дома и бани, на участке имеется сарай (подсобное помещение), расположенный рядом с гаражом, и теплица, построенная на территории огорода (огород отмечен цифрой 2). Перед жилым домом имеются яблоневые посадки.

Все дорожки внутри участка имеют ширину 1 м и вымощены тротуарной плиткой размером 1 м × 1 м. Между баней и гаражом имеется площадка площадью 64 кв. м, вымощенная такой же плиткой.

К домохозяйству подведено электричество. Имеется магистральное газоснабжение.

1 задание

Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в ответ запишите последовательность четырех цифр.

Объекты	жилой дом	сарай	баня	теплица
Цифры

Решение

Заметим, что по тексту жилой дом находится в глубине территории, также перед ним имеются яблоневые посадки. Жилой дом обозначен цифрой 3. Гараж обозначен на рисунке цифрой 7. Сарай расположен рядом с гаражом. Значит, сарай обозначен цифрой 4. При входе на участок баня находится справа от ворот, значит, баня обозначена цифрой 6. Теплица находится на территории огорода, следовательно, теплица обозначена на рисунке цифрой 1.

Ответ: 3461.

2 задание

Тротуарная плитка продается в упаковках по 4 штуки. Сколько упаковок плитки понадобилось, чтобы выложить все дорожки и площадку перед гаражом?

Решение

Заметим, что, поскольку одна плитка имеет площадь 1 м², для площадки перед гаражом понадобится 64 плитки. Для того, чтобы выложить все дорожки, понадобится еще 26 плиток. Значит, всего необходимо 90 плиток. Теперь найдём, сколько упаковок плитки понадобилось:

$\frac{90}{4}=22,5$

Следовательно, чтобы выложить все дорожки и площадку перед гаражом понадобится 23 упаковки плитки.

Ответ: 23.

3 задание

Найдите площадь, которую занимает жилой дом. Ответ дайте в квадратных метрах.

Решение

Сторона одной клетки равна 2 м. Значит, площадь жилого дома равна:

3*5*2*2+2*1*2*2=68 м²

Ответ: 68.

4 задание

Найдите расстояние от жилого дома до гаража (расстояние между двумя ближайшими точками по прямой) в метрах.

Решение

Найдем расстояние между двумя ближайшими точками по прямой жилого дома и гаража по теореме Пифагора:

$\sqrt{6^{2}+8^{2}}=\sqrt{100}=10$

Ответ: 10.

5 задание

Хозяин участка планирует устроить в жилом доме зимнее отопление. Он рассматривает два варианта: электрическое или газовое отопление. Цены на оборудование и стоимость его установки, данные о расходе газа, электроэнергии и их стоимости даны в таблице.

	Нагреватель (котел)	Прочее оборудование и монтаж	Сред. расход газа / сред. потребл. мощность	Стоимость газа / электрэнергии
Газовое отопление	24 тыс. руб.	18 280 руб.	1,2 куб. м/ч	5,6 руб./куб. м
Электр. отопление	20 тыс. руб.	15 000 руб.	5,6 кВт	3,8 руб./(кВт · ч )

Обдумав оба варианта, хозяин решил установить газовое оборудование. Через сколько часов непрерывной работы отопления экономия от использования газа вместо электричества компенсирует разность в стоимости покупки и установки газового и электрического отопления?

Решение

Чтобы установить газовое оборудование, понадобится 24 000 + 18 280 = 42 280 руб. Для установки электрического оборудования понадобится 20 000 + 15 000 = 35 000 руб. Разница в стоимости составляет 42 280 − 35 000 = 7 280 руб. Час обогрева газом стоит 5,6 · 1,2 = 6,72 руб./ч. Час обогрева электричеством стоит 5,6 · 3,8 = 21,28 руб./ч. Разница в стоимости составляет 21,28 − 6,72 = 14,56 руб./ч. Значит, экономия от использования газа вместо электричества компенсирует разность в стоимости установки газового и электрического отопления через:

$\frac{7280}{14,56}=500 \textbf{ }\textbf{часов}$

Ответ: 500.

Подготовьтесь к ЕГЭ или ОГЭ за 4 месяца

Интенсивный онлайн курс в Годографе с экспертами МЦКО

Узнать подробнее

Ответы на часто задаваемые вопросы

Что нужно знать для решения практико ориентированных задач по математике?

Основные определения и формулы площади фигур, признаки подобия и равенства треугольников, их соотношения.

Как выглядит практико ориентированная задача из ОГЭ?

Практико-ориентированные задачи моделируют жизненные ситуации, поэтому в них встречаются знакомые всем люди, здания, условия. Обычно требуется найти площадь, расстояние, рассчитать количество стройматериалов и пр.

Все статьи