Треугольники ОГЭ по математике
Простой ответ, что включено в 15 задание ОГЭ по математике
Тема треугольников в ОГЭ по математике охватывает все важные определения и формулы площади различных фигур. Важно знать и уметь применять свойства треугольников, а также ориентироваться в понятиях синуса, косинуса, тангенса прямоугольного треугольника.
Прямоугольные треугольники – разбор 15 задания ОГЭ по математике
Треугольник называется прямоугольным, если один из его углов прямой, то есть равен 90º. Стороны, прилежащие к прямому углу, называются катетами, а сторона, лежащая против прямого угла — гипотенуза.
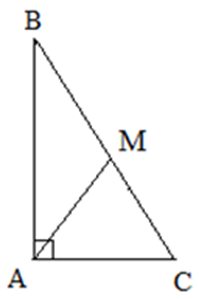
Свойства прямоугольного треугольника:
- Сумма острых углов треугольника равна 90º.
- Гипотенуза прямоугольного треугольника больше каждого из катетов.
- Катет, лежащий против угла в 30°, равен половине гипотенузы.
- Две высоты прямоугольного треугольника совпадают с его катетами.
- Центр описанной окружности прямоугольного треугольника лежит
в середине гипотенузы. - Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.
Теорема Пифагора. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:
![]()
Понятие синуса, косинуса, тангенса прямоугольного треугольника – задание 15 ОГЭ математика 2024 теория
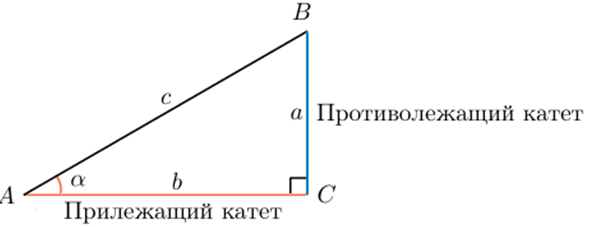
Синус острого угла в прямоугольном треугольнике — это отношение противолежащего катета к гипотенузе:
![]()
Косинус острого угла в прямоугольном треугольнике — отношение прилежащего катета к гипотенузе:
![]()
Тангенс острого угла в прямоугольном треугольнике — отношение противолежащего катета к прилежащему:
![]()
Другое (равносильное) определение: тангенсом острого угла называется отношение синуса угла к его косинусу:
![]()
Котангенс острого угла в прямоугольном треугольнике — отношение прилежащего катета к противолежащему (или, что-то же самое, отношение косинуса к синусу):
![]()
Основное тригонометрическое тождество связывает синус и косинус одного и того же угла. Сформулируем его: для любого угла справедливо:
![]()
Соотношения между сторонами и углами треугольника
Соотношения между сторонами и углами треугольника помогают сравнивать углы треугольника, зная соотношение его сторон, и наоборот.
Теорема (соотношения между сторонами и углами треугольника)
В треугольнике:
1) против большей стороны лежит больший угол;
2) против большего угла лежит большая сторона.
Теорема косинусов: Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.
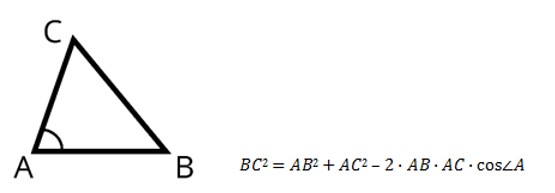
Теорема синусов: Стороны треугольника пропорциональны синусам противолежащих углов.
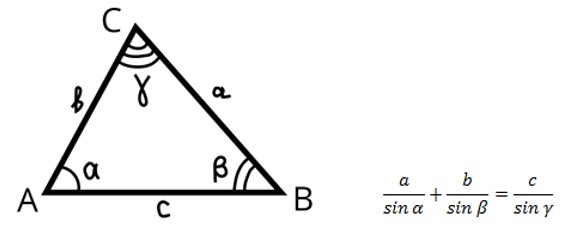
Равнобедренный треугольник – ОГЭ математика
Равнобедренный треугольник — треугольник, у которого равны две стороны. Например: AB = BC — боковые стороны; AC — основание равнобедренного треугольника.
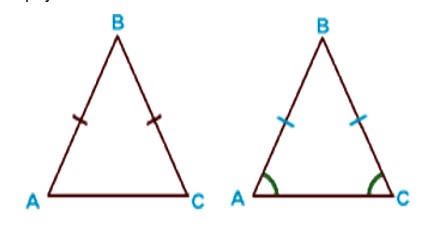
Свойства равнобедренного треугольника:
- в равнобедренном треугольнике углы при основании равны;
- в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
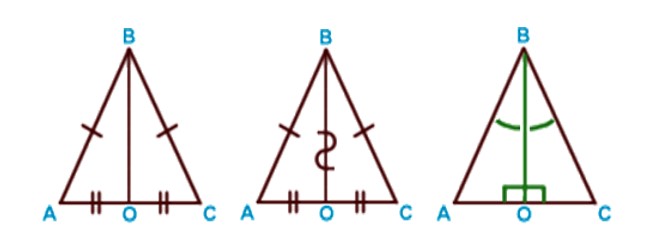
AB=BC (равнобедренный треугольник), AO=OC (BO — медиана), BO — общая сторона ΔABO и ΔCBO. ΔABO = ΔCBO по 3 признаку.
Следовательно: ∠ ABO = ∠ CBO. BO — биссектриса. ∠AOC — развернутый угол = 180°.
![]()
BO — высота.
- В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
- В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
Признаки равнобедренного треугольника:
1) если в треугольнике два угла равны, то он равнобедренный;
2) если в треугольнике биссектриса является медианой или высотой, то этот треугольник равнобедренный;
3) если в треугольнике медиана является биссектрисой или высотой, то этот треугольник равнобедренный;
4) если в треугольнике высота является медианой или биссектрисой, то этот треугольник равнобедренный.
Свойство углов равнобедренного треугольника
В равнобедренном треугольнике углы при основании равны.
Поскольку в любом треугольнике сумма углов равна 180°, то угол, противоположный основанию выражается следующим образом:
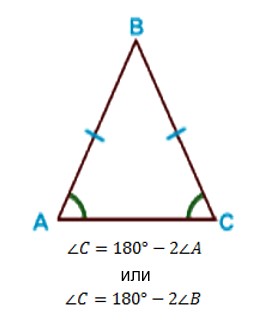
где ∠ A и ∠ B — углы при основании равнобедренного треугольника.




- Как поступить в любой вуз по олимпиаде в 2026 году.
- Бесплатный курс ЕГЭ по математике 2026 (профиль)
- Бесплатный курс ЕГЭ по русскому языку 2026
- Бесплатный курс ОГЭ по математике 2026
- 10 главных правил: Как сдать ЕГЭ на 80+ баллов


Равносторонний треугольник
Равносторонним треугольником называется треугольник, у которого все стороны равны.
Свойства равностороннего треугольника
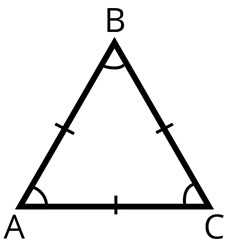
1) Все углы равностороннего треугольника равны по 60º.
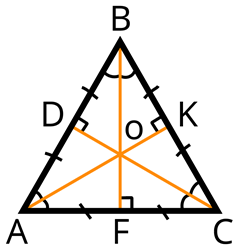
2) Высота, медиана и биссектриса, проведённые к каждой из сторон равностороннего треугольника, совпадают:
AK — высота, медиана и биссектриса, проведённые к стороне BC;
BF — высота, медиана и биссектриса, проведённые к стороне AC;
CD — высота, медиана и биссектриса, проведённые к стороне AB.
Длины всех трёх высот (медиан, биссектрис) равны между собой: AK=BF=CD
Если a — сторона треугольника, то
![]()
3) Точка пересечения высот, биссектрис и медиан называется центром правильного треугольника
и является центром вписанной и описанной окружностей (то есть в равностороннем треугольнике центры вписанной и описанной окружностей совпадают).
4) Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, считая от вершин: AO:OK=BO:OF=CO:OD=2:1
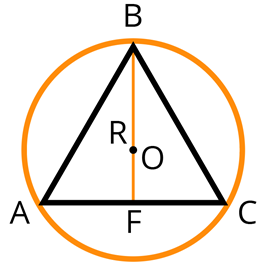
5) Расстояние от точки пересечения высот, биссектрис и медиан до любой вершины треугольника равно радиусу описанной окружности: BO=R,
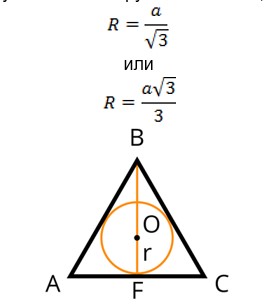
6) Расстояние от точки пересечения высот, биссектрис и медиан до любой стороны треугольника равно радиусу вписанной окружности: OF=r
![]()
или
![]()
7) Сумма радиусов вписанной и описанной окружностей правильного треугольника равна его высоте, медиане и биссектрисе: R+r=BF.
8) Радиус вписанной в правильный треугольник окружности в два раза меньше радиуса описанной окружности: R=2r.
Замечательные точки треугольника – ОГЭ математика задание 15
Первая замечательная точка треугольника
Точка пересечения биссектрис.
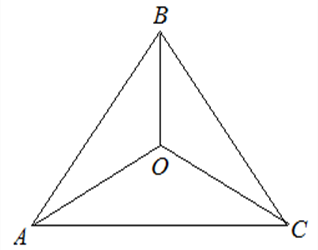
Эта точка является центром вписанной в треугольник окружности и всегда находится внутри треугольника. Данная точка равноудалена от сторон треугольника.
Вторая замечательная точка треугольника
Точка пересечения серединных перпендикуляров сторон треугольника.
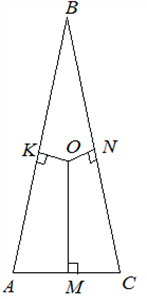
Эта точка — центр описанной около треугольника окружности, находится в треугольниках с острыми углами, вне треугольника с тупым углом и на гипотенузе прямоугольного треугольника. Данная точка равноудалена от всех вершин треугольника.
Третья замечательная точка треугольника
Точка пересечения медиан.
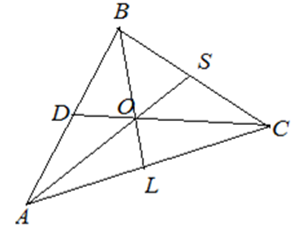
Теорема
Медианы треугольника пересекаются в одной точке, которая делит каждую медиану
в отношении 2:1, считая от вершины.
Точка пересечения медиан является центром тяжести треугольника.
Четвёртая замечательная точка треугольника
Точка пересечения высот треугольника.
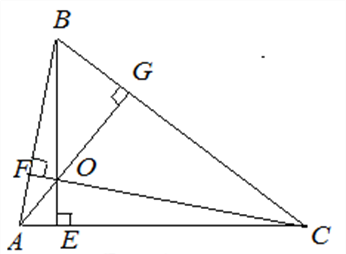
Теорема
Высоты треугольника или их продолжения пересекаются в одной точке.
Точку пересечения высот называется ортоцентром треугольника.
Высоты в тупоугольных треугольниках
В отличие от медианы или биссектрисы, высота треугольника может быть расположена как внутри треугольника, так и вне его.
В тупоугольном треугольнике внутри треугольника лежит только одна высота — та, которая проведена из вершины тупого угла.
Две другие высоты лежат вне треугольника и опущены к продолжению сторон треугольника.
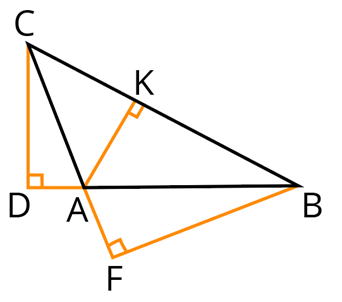
AK — высота, проведенная к стороне BC.
BF — высота, проведенная к продолжению стороны АС.
CD — высота, проведенная к продолжению стороны AB.
Точка пересечения высот тупоугольного треугольника также находится вне треугольника:
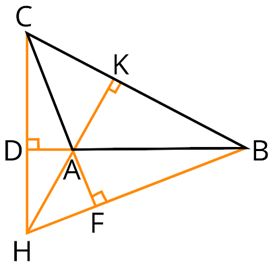
Точка H — ортоцентр треугольника ABC.
Площадь треугольника
Первая формула
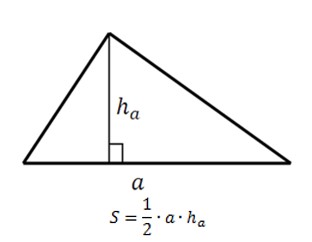
Площадь треугольника равна половине произведения длины основания и высоты, опущенной на это основание.
Формула вторая
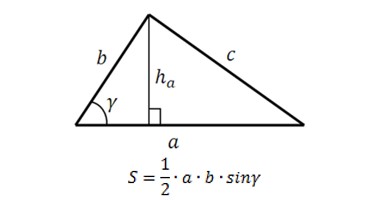
Площадь треугольника равна половине произведения его соседних сторон на синус угла между ними.
Формула Герона (третья)
![]()
Формула четвёртая
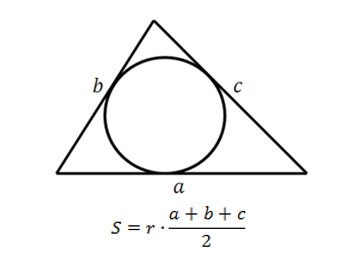
где r — радиус вписанной окружности
Формула пятая
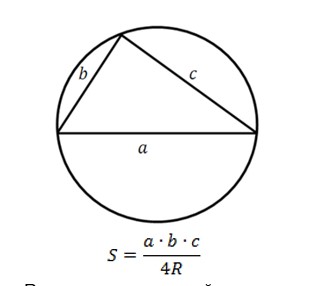
где R — радиус описанной окружности.
Прототипы задания 15 ОГЭ математика 2024
Задача 1
Сторона равностороннего треугольника равна . Найдите высоту этого треугольника.
Решение
Так как треугольник ABC равносторонний, то его высота BH является и медианой, и биссектрисой. Тогда треугольник ABH — прямоугольный. Тогда:
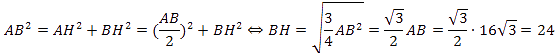
Ответ: 24.
Задача 2
В треугольнике ABC AB = BC, а высота AH делит сторону BC на отрезки BH=64, CH=16. Найдите cosB.
Решение
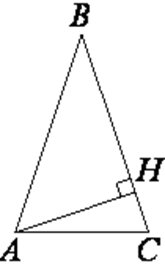
Из треугольника ABH по определению косинуса:
![]()
Ответ: 0,8.
Задача 3
В треугольнике ABC угол C прямой, AC=9, cosA=0,3. Найдите AB.
Решение
Треугольник ABC — прямоугольный. Таким образом
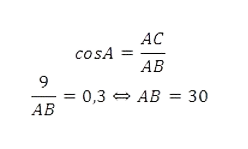
Ответ: 30.
Задача 4
Площадь прямоугольного треугольника равна
![]()
Один из острых углов равен 30°. Найдите длину гипотенузы.
Решение
Пусть x — длина катета, лежащего против угла в 30°, тогда гипотенуза равна 2x, второй катет равен
![]()
Площадь прямоугольного треугольника равна половине произведения катетов.
![]()
Следовательно, длина гипотенузы, равна 16.
Ответ: 16.
Ответы на часто задаваемые вопросы

Что представляет собой 11 задание ОГЭ по математике 2024? В 11 задании ОГЭ по математике 2024 идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции…

Как оформлять 21 задание ОГЭ по математике Для того чтобы получить полный балл за решение 21 задачи, следует математически грамотно и полно раскрыть ответ – из него должен быть понятен…