Какие встречаются варианты 9 задания ОГЭ по математике?

Как правило, в 9 задании идет речь о линейных уравнениях с одной переменной. Для их успешного решения нужно знать основы алгебры: раскрывать скобки, приводить к общему знаменателю и выражать неизвестные в уравнении.

9 задание ОГЭ по математике – теория

Тождественные преобразования уравнений:

Перенос слагаемых из одной части уравнения в другую с изменением их знаков на противоположные.

Умножение и деление обеих частей уравнения на одно и то же ненулевое число.

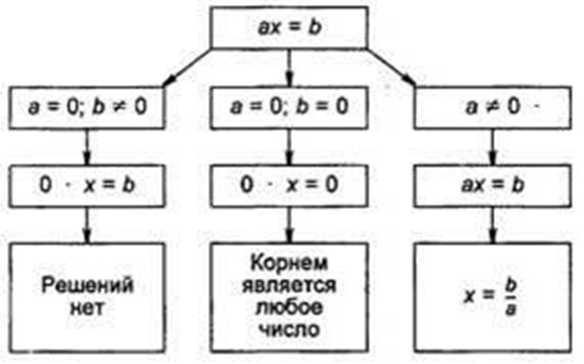
Какое число решений может иметь линейное уравнение?

Большинство учеников 9 класса умеют легко раскрывать скобки, приводить к общему знаменателю и выражать неизвестные в уравнении. Однако не мешает перестраховаться и повторить пройденный материал.

Для начала решите следующее линейное уравнение: 7x+3(8-x)=6. Если вы уверенно получили в ответе -4,5, то можем двигаться дальше. Будет нелишним повторить, как решаются квадратные уравнения. Вот несколько примеров:

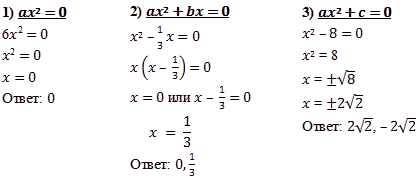
Для подготовки к ОГЭ по математике задание 9 стоит показать вывод формулы дискриминанта квадратного уравнения: для этого в квадратном уравнении выделяем полный квадрат, берем корень от обеих частей и выражаем неизвестную.

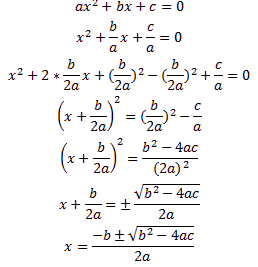
Также стоит рассказать про формулу D1=k²-ac , где: 

Тогда корни уравнения будут находиться по формуле:

Данная формула может позволить уменьшать расчеты как минимум в трех заданиях экзамена.

Аналогично можно объяснить теорему о том, что квадратный многочлен, имеющий 2 решения в нуле, разбивается на множители. Скажем, если у нас есть квадратное уравнение с одним из корней x = 3. Тогда, подставив x = 3, мы получим ноль. Скажите, а в каком еще случае мы будем получать ноль в любом уравнении при подстановке x = 3? Мы тоже будем получать ноль, если у нас в уравнении есть множитель x – 3. Тогда при x = 3 всё уравнение станет равно нулю.

А не значит ли это, что квадратное уравнение, которое при x = 3 обращается в ноль, можно преобразовать, «выделив» из него множитель x–3? Если это предположение верно, оно должно работать для обоих корней, то есть тогда можно выделить множители  x-x₁ и x—x₂. Если мы просто перемножим их, то получим x², а не ax², как в квадратном уравнении общего вида. Поэтому давайте попробуем, перемножив их, умножить еще на a:

это должно быть равно x²+bx+c.

Если теперь раскрыть скобки и разделить всё на a, мы узнаем знакомую теорему Виета:

Разница в том, что таким образом мы не даем «истину свыше», пытаясь потом показать, что она справедлива, а сами логически к ней прийти.

Варианты 9 задания – ОГЭ по математике

Ответы к заданиям:

1. Ответ: -4,5.
2. Ответ: -1.
3. Ответ: -3.
4. Ответ: 4.
5. Ответ: 1.
6. Ответ: 1,5.