8bit > Математика ОГЭ > Графики функций ОГЭ по математике

Графики функций ОГЭ по математике

05-05-2023

Дополнительные темы

Демоверсия ОГЭ по математике 2024 года Окружность, круг, их элементы ОГЭ Треугольники ОГЭ по математике Практико-ориентированные задачи ОГЭ по математике Прогрессии ОГЭ по математике Теория вероятности в ОГЭ по математике 21 задание ОГЭ по математике 20 задание ОГЭ по математике Расчеты по формулам ОГЭ по математике Графики функций ОГЭ по математике 11 задание ОГЭ по математике 13 задание ОГЭ по математике Рациональные уравнения ОГЭ 9 задание ОГЭ по математике 7 и 8 задания ОГЭ по математике 6 задание ОГЭ по математике Демоверсия ОГЭ по математике 2023 года

Графики функций — Варианты 11 задания ОГЭ по математике – краткий ответ

Так же, как и в примерах с линейными и квадратичными функциями, ответом в задании ОГЭ по математике 11 является набор цифр, описывающий соответствие между различными объектами. Хотя на самом экзамене мы ожидаем работу именно с графиками функций, тем не менее, в некоторых заданиях дается вместо рисунков их описание. Это делается, чтобы подчеркнуть те детали, на которые надо обратить внимание при работе с графиками функций.

Функция обратной пропорциональности – решение 11 задания ОГЭ по математике

Функция обратной пропорциональности — это функция вида y=k/x . Она выражает обратную пропорциональную зависимость между x и y (k≠0 – число) — обратная пропорциональность.

k — коэффициент обратной пропорциональности.

График функции представляет собой гиперболу.

Функция имеет две асимптоты — вертикальную и горизонтальную.

Прямая линия называется асимптотой графика функции, если график функции неограниченно сближается с этой прямой при удалении точки графика в бесконечность:

x=a уравнение вертикальной асимптоты.
y=b уравнение горизонтальной асимптоты.
y=kx+b уравнение наклонной асимптоты.

Ветви гиперболы располагаются в I и III координатных четвертях, если k>0 и во II и IV четвертях, если k<0 .

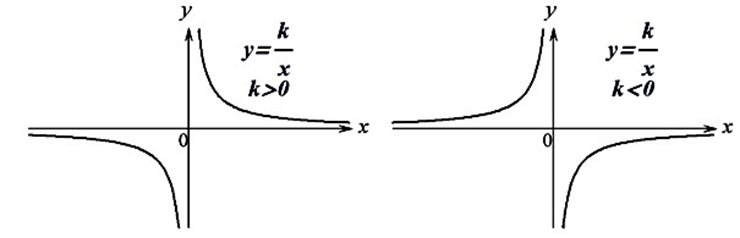
Функция обратной пропорциональности огэ

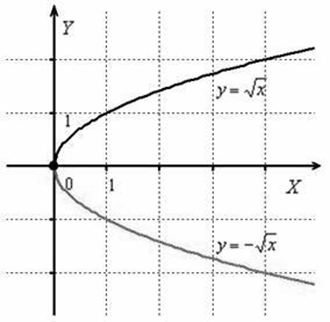
Функция арифметического квадратного корня – ОГЭ математика графики функций задания

Областью определения этой функции является множество неотрицательных действительных чисел, так как выражение x² имеет значение только при x≥0.

Для построения графика данной функции возьмем такие значения x , из которых можно легко извлечь квадратный корень. Причём, если дана функция

$y=\sqrt{x}$

то её график располагается в I координатной четверти;

если

$y=\sqrt{x}$

то в IV.

ОГЭ математика графики функций

При решении задачи, где нужно соотнести график и функцию, естественно, пользуемся знаниями о связи числовых коэффициентов функций и их графиками.

Рассмотрим несколько примеров.

Пример 1.

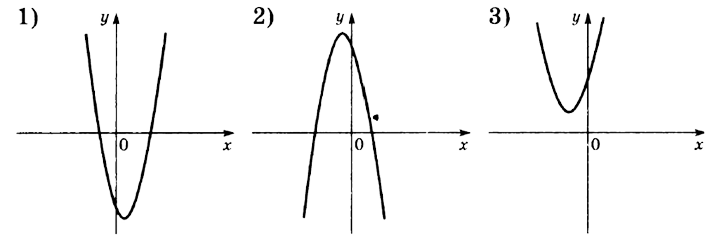
На рисунках изображены графики функций вида y=ax²+bx+c

Установите соответствие между знаками коэффициентов a и c и графиками функций.

Коэффициенты:

А) a > 0, c > 0

Б) a < 0, c > 0

В) a > 0, c < 0

Графики:

математике огэ

Решение

Мы вспоминаем, за что отвечают коэффициенты a и b при построении графиков функции вида y=ax²+bx+c. Коэффициент a определяет направление ветвей параболы: если a>0, то ветви направлены вверх, а если a<0, то ветви направлены вниз.

Таким образом, мы видим, что только у второй параболы ветви направлены вниз, а значит a<0. У первой и третьей ветви направлены вверх, то есть a>0.

Далее мы смотрим, на что влияет коэффициент c.

Коэффициент c отвечает за положение параболы относительно оси x, или же отвечает за сдвиг по оси y, а именно:

если c>0, то вершина параболы расположена выше оси x;
если c<0, то вершина параболы расположена ниже оси x.

Так, у первой параболы c<0, у второй и третьей c>0.

Из всего вышеперечисленного можно найти ответ:

А) 3

Б) 2

В) 1

Ответ: 321.

Пример 2. Установите соответствие между графиками функций и формулами, которые их задают.

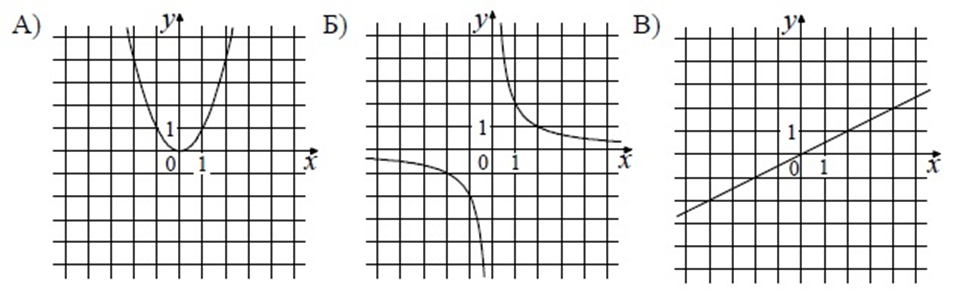
математике огэ

y=x²

$y=\frac{x}{2}$

$y=\frac{2}{x}$

Решение

Для решения данной задачи необходимо знать вид графиков функций, а именно:

y=x²

парабола, в общем виде это y=ax²+bx+c, но в нашем случае b=c=0, а a=1.

$y=\frac{x}{2}$

прямая, в общем виде график прямой имеет вид y=ax+b, в нашем случае b=0:

$a=\frac{1}{2}$

$y=\frac{2}{x}$

гипербола, в общем виде график функции:

y=\frac{a}{x}+b, в данном примере b=0, a=2.

Парабола изображена на рисунке А, гипербола на рисунке Б, а прямая — В.

Ответ: А 1, Б 3, В 2.

Ответ: 132.

Пример 3. Установите соответствие между функциями и их графиками.

Функции:

A) y=-3/x

Б) y=3/x

В) y=1/(3x)

Графики:

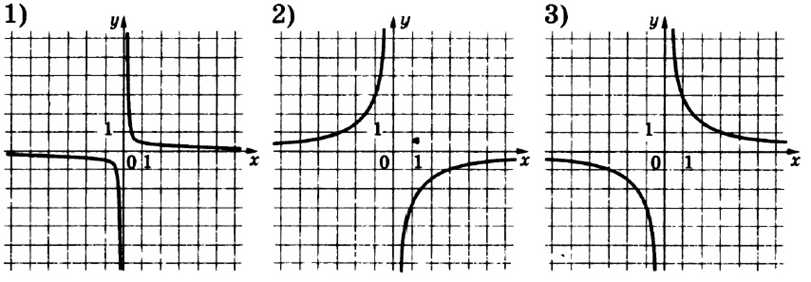
математике огэ

Решение

В данной ситуации можно воспользоваться двумя подходами. Рассмотрим первый подход — можно руководствоваться общими соображениями.

Общие правила:

если уравнение гиперболы положительное (то есть не стоит знак «–», как во втором и третьем случае), то график функции лежит в первой и третьей координатной четверти;
если перед уравнением гиперболы стоит знак как в первом случае, то график лежит во второй и четвертой четвертях.

Таким образом, можно сразу определить, что первое уравнение соответствует графику под номером 2.

А можно рассуждать так:

чем больше число в знаменателе гиперболы (рядом с x), тем сильнее гипербола жмется к осям координатной плоскости;
и наоборот: чем больше число в числителе уравнения гиперболы, тем слабее и медленнее график функции прижимается к осям.

Следовательно, функция Б слабее прижимается к осям и ей соответствует график 3, а функции В соответствует график 1, так как она сильнее прижимается к осям.

Ответ: 231.

Онлайн подготовка к ЕГЭ и ОГЭ 2025 с выгодой до 30%

Занятия в мини-группах с экспертами ЕГЭ по всем школьным предметам

Узнать подробнее

Дополнительный алгоритм решения 11 задания ОГЭ по математике

Есть алгоритм, который можно и нужно использовать для самопроверки (работает только когда четко можно определить координаты точек, принадлежащих функции, на графике). Рассмотрим, как решить задачу способом подстановки.

Решение. Рассмотрим, например, 2 рисунок и возьмём точку с координатами (3; –1), принадлежащую графику. Подставим значение x=3 в каждое уравнение и найдем y .

Получим:

$y=-\frac{3}{x}*y(3)=-\frac{3}{3}=-1$

подходит

$y=\frac{3}{x}*y(3)=\frac{3}{3}=1$

не подходит

$y=\frac{1}{3x}*y(3)=\frac{1}{3*3}=\frac{1}{9}$

не подходит

Итак, функции под буквой А соответствует график на рисунке 2.

Теперь возьмём точку с координатами (3;1), принадлежащую графику на рисунке 3. Подставим

и получим:

$y=-\frac{3}{x}*y(3)=-\frac{3}{3}=-1$

не подходит

$y=\frac{3}{x}*y(3)=\frac{3}{3}=1$

подходит

$y=\frac{1}{3x}*y(3)=\frac{1}{3*3}=\frac{1}{9}$

не подходит

Итак, функции под буквой Б соответствует график на рисунке 3.

А функции под буквой В соответствует график на оставшемся рисунке 1.

Ответ: 231.

Варианты 11 задания ОГЭ по математике

Задание 1

На рисунке изображены графики функций вида y = ax² + bx + c. Установите соответствие между графиками функций и знаками коэффициентов a и c.

А) a > 0, c < 0

Б) a < 0, c > 0

В) a > 0, c > 0

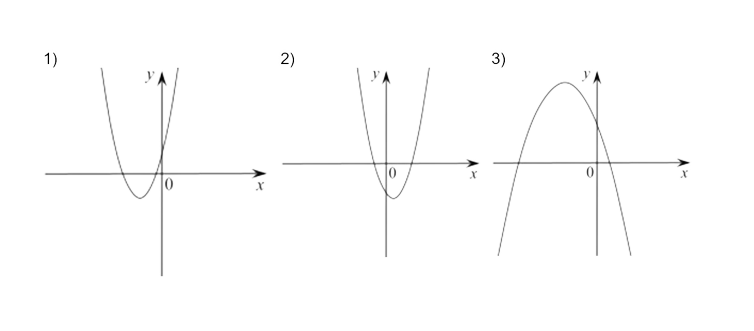
прототипы заданий огэ математика

Задание 2

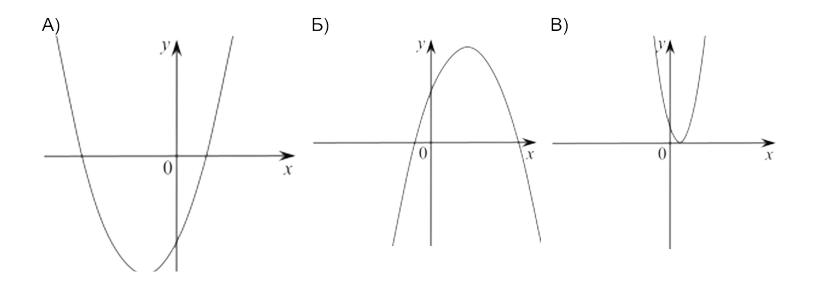
прототипы заданий огэ математика

1) a < 0, c > 0

2) a > 0, c > 0

3) a > 0, c < 0

Задание 3

На рисунке изображены графики вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.

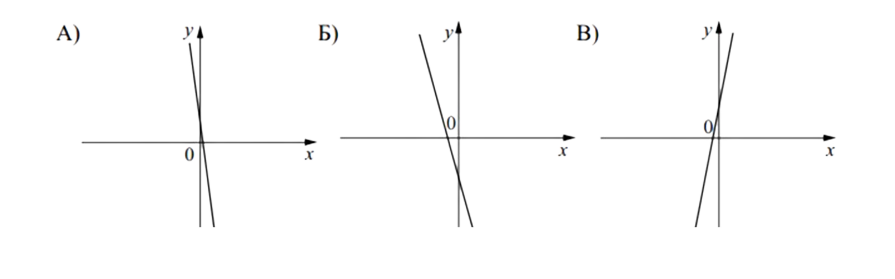
прототипы заданий огэ математика

1) k < 0, b > 0

2) k > 0, b > 0

3) k < 0, b < 0

Задание 4

На рисунке изображены графики функций вида y = kx + b. Установите соответствие между графиками функций и знаками коэффициентов k и b.

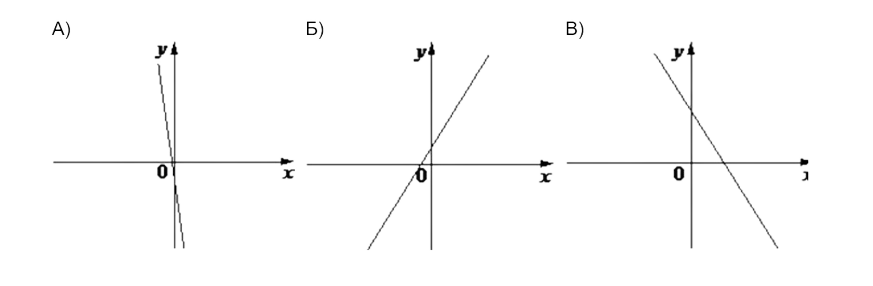
прототипы заданий огэ математика

1) k < 0, b < 0

2) k < 0, b > 0

3) k > 0, b > 0

Ответы к заданиям:

Ответ: 231.
Ответ: 312.
Ответ: 132.
Ответ: 132.

Все статьи