8bit > Математика ОГЭ > 14 задание ОГЭ по математике

14 задание ОГЭ по математике

21-05-2023

Дополнительные темы

Демоверсия ОГЭ по математике 2024 года 16 задание ОГЭ по математике – окружность, круг и их элементы 15 задание ОГЭ по математике – треугольники Практико-ориентированные задачи ОГЭ по математике 14 задание ОГЭ по математике Теория вероятностей в ОГЭ по математике 9 класс 21 задание ОГЭ по математике 20 задание ОГЭ по математике 12 задание ОГЭ по математике – расчеты по формулам Функции арифметического квадратного корня — ОГЭ по математике 11 задание ОГЭ по математике 13 задание ОГЭ по математике Рациональные уравнения ОГЭ 9 задание ОГЭ по математике 7 и 8 задания ОГЭ по математике 6 задание ОГЭ по математике Демоверсия ОГЭ по математике 2023 года

Как решать 14 задание ОГЭ по математике

Задачи на прогрессии можно разделить на два подтипа по характеру прогрессии: арифметическая и геометрическая. Задачи второго подтипа не требуют никаких знаний, кроме представления о геометрической прогрессии. Для решения же первого подтипа нужно знание пары элементарных формул и умение с ними работать.

Арифметическая прогрессия – 14 задание ОГЭ по математике 2024

Начнем с понятия арифметической прогрессии.

Арифметическая прогрессия — это последовательность (или ряд) чисел, где между соседними числами одинаковая разница, то есть, как можно более простыми словами. Вот несколько простейших примеров:

1 2 3 4 5 6 7 8 9 10

4 7 10 13 16 19

5 3 1 –1 –3 –5 –7

Важно: числа должны либо только расти, либо только уменьшаться.

В общем виде, так сказать, символами, арифметическая прогрессия обозначается обычно вот так:

a₁a₂ a₃a₄a₅a₆a₇a₈a₉a₁₀…

Если, например, рассматривается такая прогрессия: 2 5 8 11 …, то здесь a₁=2, a₂=5, a3=8 и так далее.

Элемент, стоящий в арифметической прогрессии под номером n, обозначают соответственно an.

Для решения 14 задания ОГЭ по математике необходимо знать три формулы: представления n-го элемента через первый и разность прогрессии и суммы n элементов прогрессии в двух записях:

Далее нужно сказать о том, что, как уже говорили, каждый последующий элемент отличается от предыдущего на одно и то же число. Это число называют разностью прогрессии и обозначают буквой d.

Чему равна разность в следующей арифметической прогрессии: 12 17 22 27?

Получается, a₂ =a₁+d. Точно так же, a₃ =a₂+d, a₄ =a₃+d

А на сколько отличаются элементы, стоящие через один? Например, a₃ и a₁?

На две разности a₃ =a₁+2d. Давайте продолжим для остальных элементов:

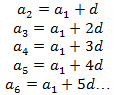
14 задание огэ математика 2023

Видите закономерность? Для того чтобы, скажем, получить 8-й элемент последовательности, нужно к первому прибавить 7 разностей; чтобы получить 15-й элемент, нужно прибавить 14 разностей.

Иначе говоря, если мы знаем первый элемент последовательности a1 и разность d, мы можем посчитать элемент под любым номером. Для того чтобы получить элемент под номером n, нужно прибавить n-1 разностей:

a_n =a₁+(n-1)d — первая формула, которую нужно записать и выучить.

Аналогично можно «обосновать» формулу суммы прогрессии.

Есть понятие суммы первых элементов прогрессии. Например, пусть есть следующая прогрессия: 3, 5, 7, 9, 11, 13, 15, 17. Если нужно найти сумму первых трех элементов, следует сложить 3 + 5 + 7; если же сумму первых 6 элементов, соответственно, 3 + 5 + 7 + 9 + 11 + 13. Обозначается сумма прогрессии буквой S:

S₃= 3 +5 +7, S₄= 3 +5 +7+9, S6= 3 +5 +7+9 +11 +13 — число внизу означает число первых элементов, которые мы суммируем.

Давайте теперь получим формулу, по которой можно рассчитывать сумму первых элементов в зависимости от . Попробуем на примере прогрессии, которую мы знаем. Скажем, нужно узнать сумму первых 9 элементов такой прогрессии:

1 2 3 4 5 6 7 8 9, S9 — ?

Можно просто «руками» сложить все 9 чисел и получить ответ. Но если мы работаем с очень большой прогрессией (скажем, больше 100 элементов), это очень долгий способ.

Заметьте вот такую штуку: 1 + 9 = 10, 2 + 8 = 10 тоже, как и 3 + 7. Складывая 1-е число слева и 1-е справа, мы получаем такую же сумму, как и складывая, скажем, 4-е число слева и справа. В сумме они равны 10, в среднем (если разделить такую пару пополам) 5. Единственное число, которое не с чем складывать — это 5, но оно как раз равно среднему!

Выходит, у арифметической прогрессии есть некоторое «среднее число», которое в этой прогрессии равно 5. И если мы сложим 9 чисел прогрессии, мы получим то же самое, как если мы сложим 9 пятёрок, проще говоря, умножим 9 на 5. Так мы тоже получим сумму прогрессии.

Вывод: для того чтобы посчитать сумму прогрессии, нужно среднее число прогрессии умножить на число элементов.

Запишем это в общем виде. Если у нас есть последовательность a₁a₂ a₃a₄a₅a₆a₇a₈a₉a₁₀… и нам нужно найти сумму первых n элементов, то есть Sn , то нужно найти среднее между 1-м и n-м элементами и умножить на n:

$S_{n}=\frac{a_{1}+ a_{n}}{2}*n$

Это вторая формула, которую вам следует знать.

Теперь, если подставить первую полученную формулу во вторую, мы получим третью формулу:

$S_{n}=\frac{2a_{1}+(n-1)d}{2}*n$

Эти три формулы нужно знать или научиться получать, чтобы решать различные задачи на последовательности из ОГЭ по математике.

Геометрическая прогрессия – ОГЭ математика

Последовательность, у которой задан первый член b1 не равный 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q не равное 0, называется геометрической прогрессией.

$b_{n+1}=b_{n}q$

где q — знаменатель прогрессии.

Формула n-го члена геометрической прогрессии:

$b_{n}=b_{1}*q^{n-1}$

Формула суммы первых n членов геометрической прогрессии:

$S_{n}=\frac{b_{1}(q^{n}-1)}{q-1}$

Бесконечно убывающая геометрическая прогрессия:

$S_{n}=\frac{b_{1}}{q-1}$

Разбор 14 задания ОГЭ по математике – прототипы

Пример 1

Бригада маляров красит забор длиной 240 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 60 метров забора. Определите, сколько дней бригада маляров красила весь забор.

Решение

Пусть бригада в первый день покрасила a₁ метров забора, во второй — a2 …, в последний — an метров забора. Тогда a₁ + a_n= 60 м, а за n дней было покрашено

S_{n}=\frac{a_{1}+a_{n}}{2}n=30n \text{ }\text{метров забора}

Поскольку всего было покрашено 240 метров забора, имеем: 30n= 240, значит n= 8. Таким образом, бригада красила забор в течение 8 дней.

Ответ: 8.

Пример 2

Улитка ползет от одного дерева до другого. Каждый день она проползает на одно и то же расстояние больше, чем в предыдущий день. Известно, что за первый и последний дни улитка проползла в общей сложности 10 метров. Определите, сколько дней улитка потратила на весь путь, если расстояние между деревьями равно 150 метрам.

Решение

Пусть улитка проползла в первый день a₁ метров, во второй — a₂, …, в последний — a_n метров. Тогда a₁ + a_n= 10 м, а за n дней проползла

S_{n}=\frac{a_{1}+a_{n}}{2}n=30n \text{ }\text{метров}

Поскольку всего она проползла 150 метров, имеем: 5n=150 откуда n=30. Таким образом, улитка потратила на весь путь 30 дней.

Ответ: 30.

Пример 3

Два приятеля положили в банк по 10000 рублей каждый, причем первый положил деньги на вклад с ежеквартальным начислением 10%, а второй — с ежегодным начислением 45%. Через год приятели получили деньги вместе с причитающимися им процентами. Кто получил большую прибыль? В ответе напишите «первый» или «второй».

Решение

Обозначим сумму, которую вложил каждый из приятелей за S₀. Через год у первого на счету будет S₀ · 1,1⁴ рублей или S₀ · 1,4641 рублей, а у второго — S₀ · 1,45 рублей. Таким образом получаем, что большую прибыль получит первый приятель.

Ответ: первый.

Пример 4

Компания «Альфа» начала инвестировать средства в перспективную отрасль в 2001 году, имея капитал в размере 5000 долларов. Каждый год, начиная с 2002 года, она получала прибыль, которая составляла 200% от капитала предыдущего года. А компания «Бета» начала инвестировать средства в другую отрасль в 2003 году, имея капитал в размере 10 000 долларов, и, начиная с 2004 года, ежегодно получала прибыль, составляющую 400% от капитала предыдущего года. На сколько долларов капитал одной из компаний был больше капитала другой к концу 2006 года, если прибыль из оборота не изымалась?

Решение

Каждый год прибыль компании «Альфа» составляла 200% от капитала предыдущего года, значит, капитал каждый год составлял 300% от капитала предыдущего года. В конце 2006 года на счёте компании «Альфа» была сумма

5000·3^2006–2001 = 5000·3⁵ = 5000·243 = 1 215 000 долларов.

Каждый год прибыль компании «Бета» составила 400% от капитала предыдущего года, значит, капитал каждый год составлял 500% от капитала предыдущего года. В конце 2006 года на счёте компании «Бета» была сумма

10 000·5^2006–2003 = 10 000 · 5³ = 10 000 · 125 = 1 250 000.

Таким образом, капитал компании «Бета» был на 35 000 долларов больше.

Ответ: 35 000.

Подготовьтесь к ЕГЭ или ОГЭ за 4 месяца

Интенсивный онлайн курс в Годографе с экспертами МЦКО

Узнать подробнее

Ответы на часто задаваемые вопросы

Что такое геометрическая прогрессия ОГЭ?

Последовательность, у которой задан первый член b_1 не равный 0, а каждый следующий равен предыдущему, умноженному на одно и то же число q не равное 0, называется геометрической прогрессией.

Что такое арифметическая прогрессия в математике?

Арифметическая прогрессия — это последовательность (или ряд) чисел, где между соседними числами одинаковая разница, то есть, как можно более простыми словами. Вот несколько простейших примеров: 1 2 3 4 5 6 7 8 9 10; 4 7 10 13 16 19; 5 3 1 –1 –3 –5 –7.

Как посчитать сумму прогрессии?

Для того чтобы посчитать сумму прогрессии, нужно среднее число прогрессии умножить на число элементов.

Все статьи