















6 задание ОГЭ по математике
Что включает 6 задание ОГЭ?
Числа на прямой и числовые неравенства – одна из первых тем, с которой нужно ознакомиться для успешного решения заданий экзамена. Речь идет об арифметических операциях с целыми и дробно-рациональными числами, классификации чисел, сравнении их на прямой.
Классификация чисел ОГЭ
Начнем с того, что у нас есть различные числа по типу, составляющие множества чисел. Сначала у нас есть числа, которыми мы считаем (количественные числительные) – они называются натуральными (N). 1, 2, 3, … Обязательно стоит запомнить, что 0 не является натуральным числом.
Натуральные числа делятся на четные или нечетные, затем простые, составные и 1. Важно отличать одни числа от других и не путать их между собой. Особенно часто бывают ошибки с классификацией чисел 0 и 1.
Хорошо, двигаемся дальше. Есть числа, которые называются целыми. Например, 99 — целое число? А 0,5 — целое? Получается, что у нас есть целые и дробные числа.
Целые числа (Z):
![]()
Дробные числа:
![]()
Дробные и целые числа вместе называются рациональными и обозначаются буквой Q.
Кроме этого, есть иррациональные числа, это всякие «неадекватные» числа:
![]()
![]()
Это числа, которые невозможно записать в виде конечной или периодической десятичной дроби.
- Рациональные + Иррациональные = Действительные (R);
- Рациональные (Q) = Дробные + Целые (Z);
- Целые (Z) = Отрицательные + 0 + Натуральные (N).
Дроби – задание 6 ОГЭ по математике
Давайте вспомним, что такое дроби и как их складывать, вычитать, умножать и делить.
Дробь — это частное двух целых чисел. Верхнее число называют числителем, нижнее — знаменателем. Дроби бывают двух видов: правильные и неправильные. Правильная дробь — та, у которой числитель меньше, чем знаменатель. Можно привести аналогию с тортом: если мы разрезали торт на 8 кусков, и у нас осталось 7 кусков, то это правильно. А, вот, если же мы разрезали его на 8 кусков, а у нас теперь 9 кусков, то это неправильно, хотя бы потому, что откуда-то взялся еще один, явно не из этого торта.
Неправильная дробь — та, у которой числитель больше или равен знаменателю.
Сложение, вычитание, умножение и деление дробей – подготовка к ОГЭ по математике 6 задание
Сложить две дроби с одинаковым знаменателем довольно просто.
![]()
Немного сложней, если дроби с разным знаменателем.
![]()
Как видите, сначала нужно привести к общему знаменателю, а потом уже сложить (вычесть).
Иногда мы можем найти способ легче, чем домножить одну дробь на знаменатель другой. Это называется поиск наименьшего общего знаменателя, то есть такого числа, которое делится и на один знаменатель, и на другой. К примеру, нам нужно сложить 2 дроби:
![]()
Вместо того, чтобы умножать 4 на 50 и 3 на 15, давайте посмотрим на знаменатели дробей: 15=3*5, 50=5*10. Мы ищем у них общие множители. Как видим, и у 15, и у 50 есть множитель 5. Тогда общим знаменателем будет 3*5*10=150 — число, которое будет делиться и на 15, и на 50 (это наглядно видно). Чтобы привести к нему, мы просто домножаем дроби на то, чего у них нет: первую дробь на 10, вторую дробь на 3:
![]()
Пример был не самым простым в плане арифметики для того, чтобы продемонстрировать, что поиск наименьшего общего знаменателя действительно упростит вам жизнь.
Примеры из 6 задания ОГЭ по математике: 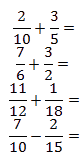
Также необходимо сказать, что смешанные дроби сначала необходимо перевести в неправильные (чаще это нужно при вычитании, так как при сложении можно просто сложить целые части, а потом разбираться с оставшимися правильными дробями).
Примеры: 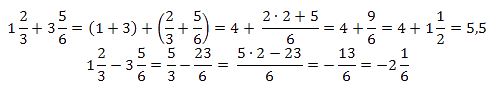
При умножении и делении дробей мы можем сокращать числитель и знаменатель и о том, что поделить — это то же самое, что умножить на перевернутую дробь.
Примеры: ![]()




- Как поступить в любой вуз по олимпиаде в 2026 году.
- Бесплатный курс ЕГЭ по математике 2026 (профиль)
- Бесплатный курс ЕГЭ по русскому языку 2026
- Бесплатный курс ОГЭ по математике 2026
- 10 главных правил: Как сдать ЕГЭ на 80+ баллов


Как решать 6 задание ОГЭ по математике — десятичные дроби
Вспоминаем про сложение, вычитание, умножение и деление десятичных дробей, а также про перевод десятичных в обыкновенные дроби и наоборот. Обыкновенные дроби нам проще умножать и делить, а десятичные наоборот проще складывать и вычитать. Складываем мы их следующим образом: поразрядно цифру с цифрой (единицы с единицами, десятую с десятой, сотую с сотой и т.д.).
Примеры:
2,341 + 1,25; 3,432 – 0,2578; 10,98 + 2,02; 30,27 – 11,12.
Умножаем и делим десятичные дроби мы столбиком, причем, внимательно следя за знаками после запятой. Сначала мы можем просто умножить числа, забыв о знаках после запятой, а потом посчитать их, сложить количество и отделить запятой. Например: 0,6*0,8=0,48 и так далее.
Сравнение чисел ОГЭ математика, числа на прямой
В этой теме встречаются несколько различных типов заданий, но все они похожи и решаются очень просто.
Первыми рассмотрим задания, в которых известно какое-то неравенство (например, число а > b) и требуется выбрать в ответе верное или неверное неравенство, в котором присутствуют числа a и b. Для наглядности рассмотрим решение примера.
Задание:
Даны положительные числа a и b, причем a < b. Выберите верное неравенство:
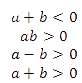
Первым делом, чтобы не запутаться, давайте возьмем вместо букв a и b числа. Так как в условии сказано, что числа положительные, пусть a = 1, b = 2 (1 < 2 подходит). Далее подставим эти числа в неравенства.
1 + 2 > 0, 3 > 0 — верно
1 — 2 > 0, –1 > 0 — неверно
1*2 < 0, 2 < 0 — неверно
9*1 — 9*2 > 0, –9 > 0 — неверно
Таким образом, чтобы решить задание такого типа, нужно взять вместо букв числа, которые будут удовлетворять условию (в нашем случае положительные числа, a < b), и подставить их в неравенства, чтобы найти верное (или неверное, в зависимости от вопроса).
Далее рассмотрим похожий тип заданий, в котором условие содержит не неравенство, а числа, расположенные на координатной прямой. Суть задания такая же.
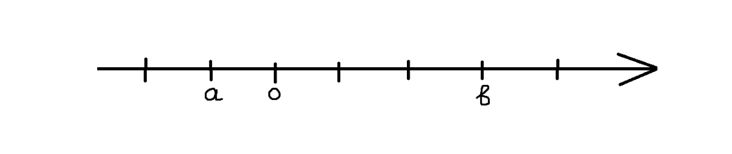
Задание:
На координатной прямой отмечены две точки. Какое из следующих утверждений верное:
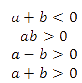
Сначала, чтобы не запутаться определим численные значения этих точек. Как видно, a = –1, b = 3. Далее подставляем эти значения в неравенства и вычисляем. Попробуйте самостоятельно посчитать и выбрать правильный ответ.
Варианты 6 задания ОГЭ по математике
Решите управление:
![]()
На координатной прямой отмечены числа a и b. В ответе укажите номер правильного варианта.
![]()
Какое из следующих утверждений является верным?
- ab>0
- a+b<0
- b(a+b)<0
- a(a+b)<0
О числах a, b, c и d известно, что:
![]()
Сравните числа d и a.
В ответе укажите номер правильного варианта.
- d=a;
- d>a;
- d<a;
- сравнить невозможно.
Какому из данных промежутков принадлежит число ? В ответе укажите номер правильного варианта.
- [0,5; 0,6];
- [0,6; 0,7];
- [0,7; 0,8];
- [0,8; 0,9].
Ответы к заданиям:
- Ответ: -2;
- Ответ: 4;
- Ответ: 2;
- Ответ: 3.
Ответы на часто задаваемые вопросы

Краткий ответ, к ак решать задания на неравенства из ОГЭ по математике Для того чтобы научиться решать задания экзамена ОГЭ, где встречаются линейные неравенства и их системы, следует основательно знать…

Что включает 6 задание ОГЭ? Числа на прямой и числовые неравенства – одна из первых тем, с которой нужно ознакомиться для успешного решения заданий экзамена. Речь идет об арифметических операциях…