















11 задание ОГЭ по математике
Что представляет собой 11 задание ОГЭ по математике 2024?
В 11 задании ОГЭ по математике 2024 идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции и математическим выражением (формулой). В задании сопоставляется различная информация о функциях. Необходимо находить и использовать в выполнении задания область определения функции, ее промежутки возрастания и убывания, промежутки знакопостоянства, нули функции, уметь читать графики функций.
Линейная функция – задания 11 ОГЭ по математике графики
Линейной функцией называется функция вида y=kx+b, где x – независимая переменная, k и b – любые числа.
Графиком линейной функции является прямая.
Чтобы построить график функции, нам нужны координаты двух точек, принадлежащих графику функции. Чтобы их найти, нужно взять два значения , подставить их в уравнение функции, и по ним вычислить соответствующие значения .
Например, чтобы построить график функции:
![]()
удобно взять x=0 и x=3, тогда ординаты эти точек будут равны y=2 и y=3. Получим точки A(0;2) и B(3:3). Соединим их и получим график нашей функции:
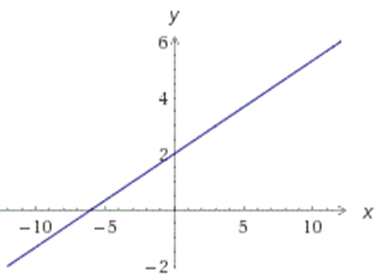
В формуле у=kx+b и число k называется коэффициентом пропорциональности, причем:
- Если k>0, то функция y=kx+b возрастает.
- Если k<0 , то y=kx+b функция убывает.
Коэффициент b показывает смещение графика функции вдоль оси OY:
- Если b>0, то график функции y=kx+b получается из графика функции y=kx сдвигом на b единиц вверх вдоль оси OY.
- Если b<0, то график функции получается из графика функции y=kx+b сдвигом на b единиц вниз вдоль оси OY.
На рисунке ниже изображены графики функций .
![]()
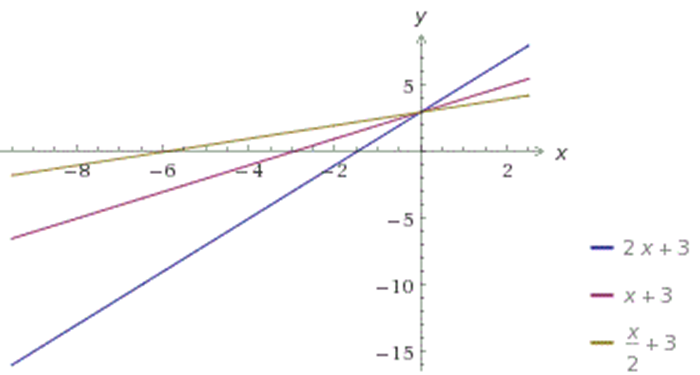
Заметим, что во всех этих функциях коэффициент k больше нуля, и функции являются возрастающими. Причем, чем больше значение k, тем больше угол наклона прямой к положительному направлению оси OY. Во всех функциях b=3— и мы видим, что все графики пересекают ось OY в точке (0;3).
Теперь рассмотрим графики функций:
![]()
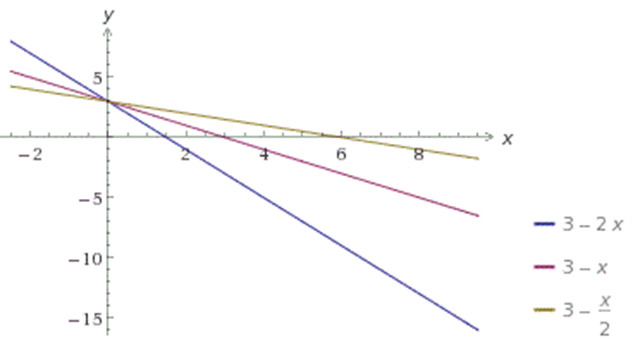
На этот раз во всех функциях коэффициент меньше нуля, и функции убывают. Коэффициент b=3, и графики также как в предыдущем случае пересекают ось OY в точке (0;3).
Рассмотрим графики функций:
![]()
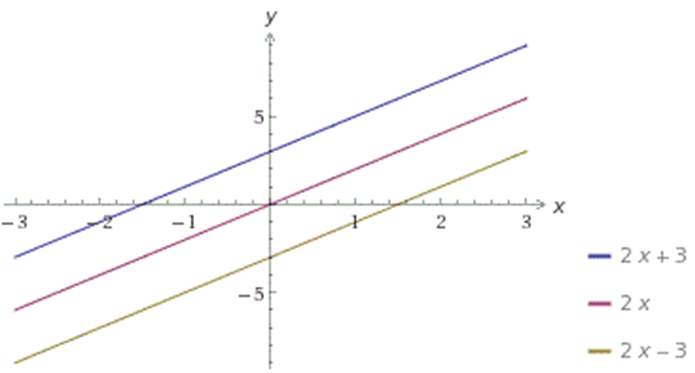
Теперь во всех уравнениях функций коэффициенты k равны 2, и мы получили три параллельные прямые.
Но коэффициенты b различны, и эти графики пересекают ось OY в различных точках:
- График функции y=2x+3(b=3) пересекает ось OY в точке (0; 3).
- График функции y=2x(b=0) пересекает ось OY в точке (0; 0) — начале координат.
- График функции y=2x-3(b=-3) пересекает ось OY в точке (0; –3).
Итак, если мы знаем знаки коэффициентов k и b, то можем сразу представить, как выглядит график функции y=kx+b.
Если k<0 и b>0, то график функции y=kx+b имеет вид:
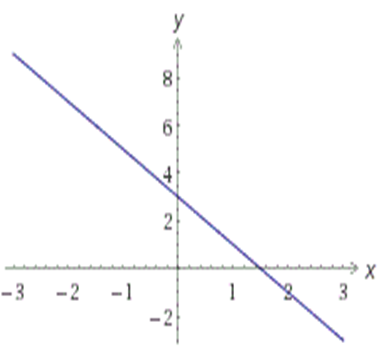
Если k>0 и b>0, то график функции y=kx+b имеет вид:
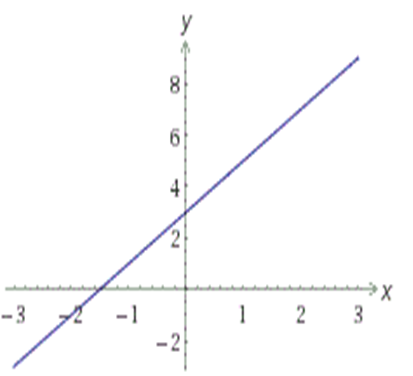
Если k>0 и b<0, то график функции y=kx+b имеет вид:
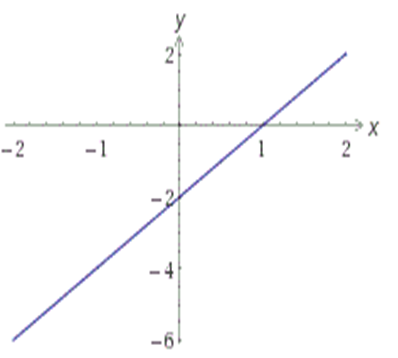
Если k<0 и b<0, то график функции y=kx+b имеет вид:
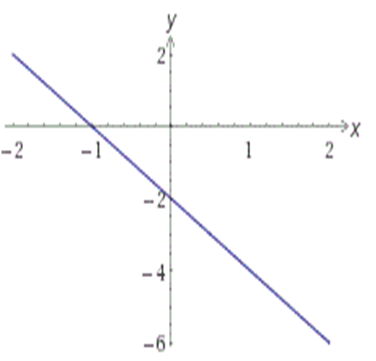
Если k=0, то функция y=kx+b превращается в функцию y=b и ее график имеет вид:
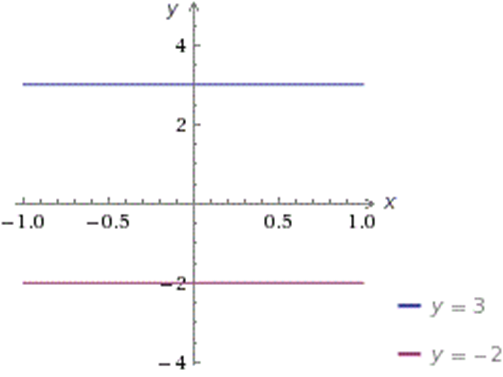
Ординаты всех точек графика функции y=b равны b. Если b=0, то график функции y=kx (прямая пропорциональность) проходит через начало координат:
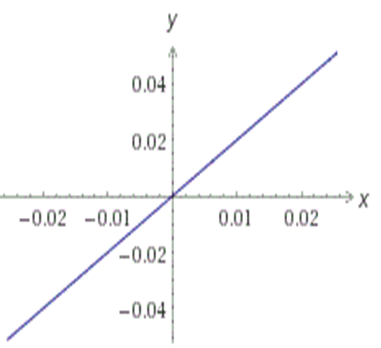
Отдельно отметим график уравнения x=a. График этого уравнения представляет собой прямую линию, параллельную оси OX, все точки которой имеют абсциссу x=a.
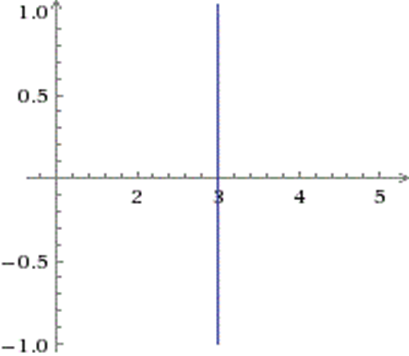
Например, график уравнения x=3 выглядит так:
Внимание! Уравнение x=a не является функцией, так одному значению аргумента соответствуют разные значения функции, что не соответствует определению функции.
Условие параллельности двух прямых:
График функции y=k1x+b1 параллелен графику функции y=k2x+b2, если k1=k2.
Условие перпендикулярности двух прямых:
График функции y=k1x+b1 перпендикулярен графику функции y=k2x+b2, если k1* k2 =-1 или k1 =-1/k2
Точки пересечения графика функции y=kx+b с осями координат С осью OY: Абсцисса любой точки, принадлежащей оси OY, равна нулю. Поэтому, чтобы найти точку пересечения с осью OY нужно в уравнение функции вместо х подставить ноль.
Получим y=b. То есть точка пересечения с осью OY имеет координаты (0; b).
С осью OX: Ордината любой точки, принадлежащей оси равна нулю. Поэтому, чтобы найти точку пересечения с осью OX нужно в уравнение функции вместо y подставить ноль.
Получим 0=kx+b. Отсюда x=-b/k. То есть точка пересечения с осью OX имеет координаты:
![]()
Квадратичная функция – виды 11 задания ОГЭ по математике
Квадратичной функцией называется функция вида y=ax2+bx+c , где a,b,c — числа, причем a≠0.
Графиком квадратичной функции является парабола.
Чтобы построить график функции y=x2, составим таблицу значений
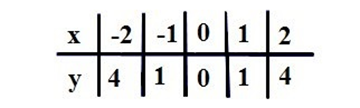
и построим график, используя полученные точки:
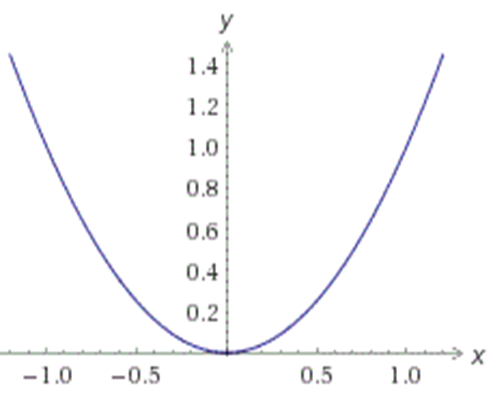
Внимание! Если в уравнении квадратичной функции старший коэффициент a=1, то график квадратичной функции имеет ровно такую же форму, как график функции y=x2 при любых значениях остальных коэффициентов.
График функции y=-x2 имеет вид:
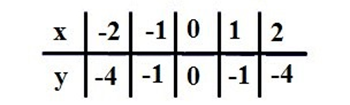
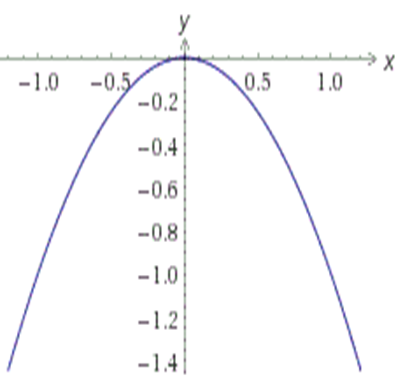
Итак:
- Если старший коэффициент a>0, то ветви параболы направлены вверх.
- Если старший коэффициент a<0, то ветви параболы направлены вниз.
Второй этап построения графика функции — значения x, в которых функция равна нулю, или нули функции. На графике нули функции f(x) — это точки пересечения графика функции y=f(x) с осью OX.
Поскольку ордината y любой точки, лежащей на оси OX равна нулю, чтобы найти координаты точек пересечения графика функции y=f(x) с осью OX, нужно решить уравнение f(x)=0.
В случае квадратичной функции y=ax2+bx+c нужно решить квадратное уравнение ax2+bx+c=0.
В процессе решения квадратного уравнения мы находим дискриминант:
![]()
который определяет число корней квадратного уравнения.
И здесь возможны три случая:
1.Если D<0, то уравнение ax2+bx+c=0 не имеет решений, и, следовательно, парабола y=ax2+bx+c не имеет точек пересечения с осью OX. Если a>0, то график функции выглядит примерно так:
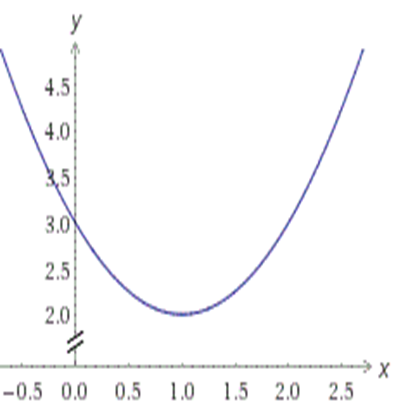
2. Если D=0, то уравнение ax2+bx+c=0 имеет одно решение, и, следовательно, парабола y=ax2+bx+c имеет одну точку пересечения с осью OX. Если a>0, то график функции выглядит примерно так:
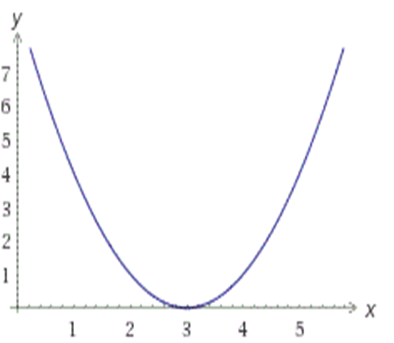
3. Если D>0, то уравнение ax2+bx+c=0 имеет два решения, и, следовательно, парабола y=ax2+bx+c имеет две точки пересечения с осью OX:
![]()
Если a>0, то график функции выглядит примерно так:
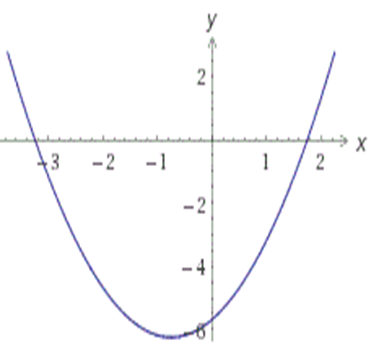
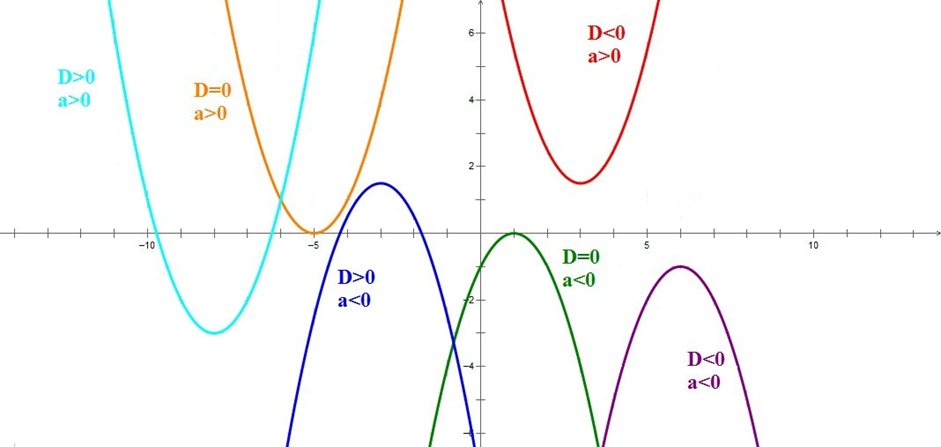
Значит, зная направление ветвей параболы и знак дискриминанта, мы уже можем в общих чертах определить, как выглядит график нашей функции.




- Как поступить в любой вуз по олимпиаде в 2026 году.
- Бесплатный курс ЕГЭ по математике 2026 (профиль)
- Бесплатный курс ЕГЭ по русскому языку 2026
- Бесплатный курс ОГЭ по математике 2026
- 10 главных правил: Как сдать ЕГЭ на 80+ баллов


Координаты вершины параболы – разбор 11 задания ОГЭ по математике 2024
Следующий важный этап построения графика квадратичной функции — координаты вершины параболы:
Прямая, проходящая через вершину параболы параллельно оси OY, является осью симметрии параболы.
И еще один этап построения графика функции — точка пересечения параболы y=ax2+bx+c с осью OY.
Поскольку абсцисса любой точки, лежащей на оси OY равна нулю, чтобы найти точку пересечения параболы y=ax2+bx+c с осью OY, нужно в уравнение параболы вместо x подставить ноль: y(0)=c.
То есть точка пересечения параболы с осью OY имеет координаты (0; c).
Итак, основные моменты построения графика квадратичной функции показаны на рисунке:
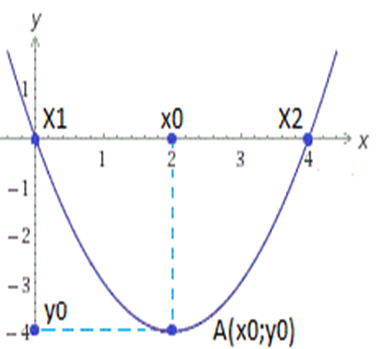
Подведем итоги по коэффициентам квадратичной функции:
- a — отвечает за направление ветвей параболы;
- b — определить его знак можно, если знать знак абсциссы вершины параболы и знак коэффициента a;
- c — отвечает за точку пересечения параболы с осью OY (похож на коэффициент b в линейной функции).
Прототип 11 задания ОГЭ по математике
Задание 1
Найдите значение b по графику функции y=ax2+bx+c, изображенному на рисунке.
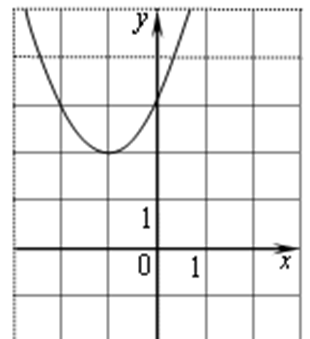
- –2;
- 1;
- 2;
- 3.
Задание 2
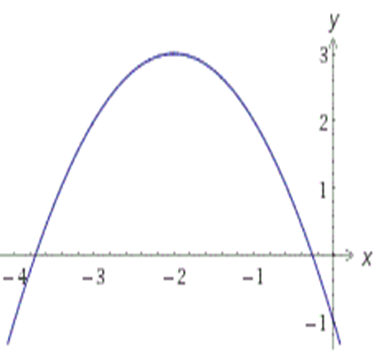
На рисунке изображён график квадратичной функции y = f(x).
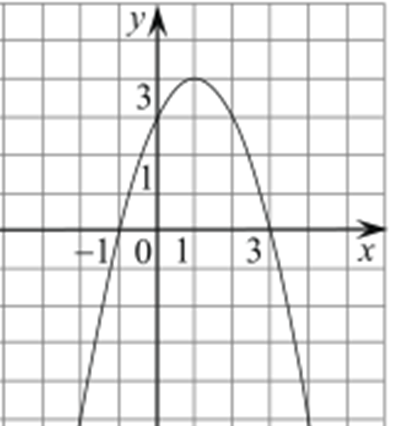
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
- f(x) < 0 при x < 1
- Наибольшее значение функции равно 3
- f(0) > f(4)
Задание 3
На одном из рисунков изображен график функции y=x2+2x-3. Укажите номер этого рисунка.

Ответы к заданиям
- Ответ: 3.
- Ответ: 12.
- Ответ: 4.
Ответы на часто задаваемые вопросы

Какие встречаются варианты 9 задания ОГЭ по математике? Как правило, в 9 задании идет речь о линейных уравнениях с одной переменной. Для их успешного решения нужно знать основы алгебры: раскрывать…

Что представляет собой 11 задание ОГЭ по математике 2024? В 11 задании ОГЭ по математике 2024 идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции…