8bit > Математика ОГЭ > 7 и 8 задания ОГЭ по математике

7 и 8 задания ОГЭ по математике

Q: Что такое рациональные числа – разбор 8 задания ОГЭ?

Рациональные числа — это числа, которые можно представить в виде дроби с целым числителем и натуральным знаменателем, есть, где m — целое, а n — натуральное. Рациональные числа могут быть представлены конечным или бесконечным десятичным периодическим дробью. Множество рациональных чисел обозначается большой латинской буквой Q.

Q: Что представляют собой иррациональные числа – ОГЭ по математике?

Иррациональными называются числа, которые нельзя представить в виде дроби, где m — целое, а n — натуральное. Иррациональные числа могут быть представлены бесконечными непериодическими дробями.

26-04-2023

Дополнительные темы

Демоверсия ОГЭ по математике 2024 года Окружность, круг, их элементы ОГЭ Треугольники ОГЭ по математике Практико-ориентированные задачи ОГЭ по математике Прогрессии ОГЭ по математике Теория вероятности в ОГЭ по математике 21 задание ОГЭ по математике 20 задание ОГЭ по математике Расчеты по формулам ОГЭ по математике Графики функций ОГЭ по математике 11 задание ОГЭ по математике 13 задание ОГЭ по математике Рациональные уравнения ОГЭ 9 задание ОГЭ по математике 7 и 8 задания ОГЭ по математике 6 задание ОГЭ по математике Демоверсия ОГЭ по математике 2023 года

Как решать задание 7 ОГЭ по математике 2024?

В первую очередь в 7 и 8 заданиях ОГЭ нужно уметь возводить числа в натуральную или целую степень. После этого выполняются простейшие арифметические вычисления и выбирается правильный ответ из предложенных вариантов.

Возведение в степень ОГЭ

Начать следует с объяснения, что называют возведением в степень. Вот соответствующее определение.

Возведение в степень — это нахождение значения степени числа.

Таким образом, нахождение значение степени числа a с показателем r и возведение числа a в степень r — это одно и то же. Например, если поставлена задача «вычислите значение степени (0,5)⁵», то ее можно переформулировать так: «Возведите число 0,5 в степень 5».

Теперь можно переходить непосредственно к правилам, по которым выполняется возведение в степень.

Возведение в натуральную степень

По определению степень числа a с натуральным показателем n равна произведению n множителей, каждый из которых равен a. Таким образом, чтобы возвести число a в степень n, нужно вычислить произведение.

Отсюда ясно, что возведение в натуральную степень базируется на умении выполнять умножение чисел, а этот материал охвачен в статье умножение действительных чисел. Рассмотрим решения нескольких примеров.

Примеры, как решать задание 7 ОГЭ математика 2024 года

Пример 1.

Выполните возведение числа −2 в четвертую степень.

Решение.

По определению степени числа с натуральным показателем имеем (−2)⁴=(−2)·(−2)·(−2)·(−2). Осталось лишь выполнить умножение целых чисел: (−2)·(−2)·(−2)·(−2)=16.

Ответ: (−2)⁴=16.

Пример 2.

Найдите значение степени

$(3\frac{2}{7})^{2}$

Решение.

Данная степень равна произведению вида:

$(3\frac{2}{7}) * 3\frac{2}{7})$

Вспомнив, как выполняется умножение смешанных чисел, заканчиваем возведение в степень:

Ответ:

$10\frac{39}{49}$

Что касается возведения в натуральную степень иррациональных чисел, то его проводят после предварительного округления основания степени до некоторого разряда, позволяющего получить значение с заданной степенью точности. Например, пусть нам требуется возвести число пи в квадрат. Если округлить число пи до сотых, то получим:

Если взять

$\pi\sim 3,14159$

Возведение в степень даст:

В заключение этого пункта отдельно остановимся на возведении в первую степень. Здесь достаточно знать, что число a в первой степени — это есть само число a, то есть а¹=а

Например:

(-9)¹=-9

Возведение в целую степень – ОГЭ по математике 7 класс задание 7

Возведение в целую степень удобно рассматривать для трех случаев: для целых положительных показателей, для нулевого показателя и для целых отрицательных показателей степени.

Так как множество целых положительных чисел совпадает со множеством натуральных чисел, то возведение в целую положительную степень есть возведение в натуральную степень. А этот процесс мы рассмотрели в предыдущем пункте.

Переходим к возведению в нулевую степень. Мы знаем, что нулевая степень числа определяется для любого отличного от нуля действительного числа a, при этом а⁰=1.

Таким образом, возведение любого отличного от нуля действительного числа в нулевую степень дает единицу.

Например:

а⁰ не определяется.

Свойства степеней – теория для 7 задания ОГЭ по математике

Теперь запишем все свойства степеней:

свойства степеней

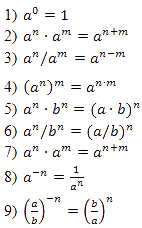
Чтобы закончить с возведением в целую степень, осталось разобраться со случаями целых отрицательных показателей. Мы знаем, что степень числа а с целым отрицательным показателем -z определяется как дробь вида:

$\frac{1}{a^z}$

В знаменателе этой дроби находится степень с целым положительным показателем. Осталось лишь рассмотреть несколько примеров возведения в целую отрицательную степень.

Пример.

Вычислите значение степени числа 3 с целым отрицательным показателем -2.

Решение.

По определению степени с целым отрицательным показателем имеем:

$2^{-3}=\frac{1}{2^{8}}$

Значение степени в знаменателе легко находится:

$2^{3}=2*2*2=8$

Таким образом:

Ответ:

$\frac{1}{8}$

Онлайн подготовка к ЕГЭ и ОГЭ 2025 с выгодой до 30%

Занятия в мини-группах с экспертами ЕГЭ по всем школьным предметам

Узнать подробнее

Формулы сокращенного умножения разбор 8 задания ОГЭ по математике

Так как мы теперь все знаем о степенях, давайте поговорим о возведении выражений во вторую степень и правила раскрытия скобок.

Рассмотрим выражение:

(a+b)(a-b)

Разные преподаватели называют способ раскрытия по-разному, кто-то говорит «правило фонтанчика», еще есть вариант — «усики», мы же будем называть это «методом фейерверка». Как этот метод работает:

Возведение суммы в квадрат:

Арифметический квадратный корень

Начнем с определения квадратного корня.

Квадратный корень из числа a — это число, квадрат которого равен a.

Чтобы привести примеры квадратных корней, возьмем несколько чисел, например, 5, −0,3, 0,3, 0, и возведем их в квадрат, получим соответственно числа 25, 0,09, 0,09 и 0 (5²=5·5=25, (−0,3)²=(−0,3)·(−0,3)=0,09, (0,3)²=0,3·0,3=0,09 и 0²=0·0=0). Тогда по данному выше определению число 5 является квадратным корнем из числа 25, числа −0,3 и 0,3 есть квадратные корни из 0,09, а 0 — это квадратный корень из нуля.

Квадратный корень извлекается только из неотрицательных чисел!

Так как у квадратного корня существует два противоположных по знаку значения, это затрудняет работу с корнями. Для обеспечения однозначности был введен арифметический квадратный корень.

Арифметический квадратный корень из неотрицательного числа a — это неотрицательное число, квадрат которого равен a. То есть под арифметическим корнем стоят всегда неотрицательные числа, и при его извлечении мы получаем тоже всегда только одно неотрицательное число, а не два противоположных по знаку, как для квадратного корня.

$\sqrt{25=5}$

Для арифметического квадратного корня из числа a принято обозначение:

$\sqrt{a}$

Знак √ называется знаком арифметического квадратного корня. Его также называют знаком радикала. Поэтому можно часть слышать как «корень», так и «радикал», что означает один и тот же объект.

Число под знаком арифметического квадратного корня называют подкоренным числом, а выражение под знаком корня — подкоренным выражением, при этом термин «подкоренное число» часто заменяют на «подкоренное выражение». Например:

$\sqrt{151}$

в записи число 151 — это подкоренное число, а в записи выражение a является подкоренным выражением.

При чтении слово «арифметический» часто опускается, например:

$\sqrt{729}$

запись читают как «квадратный корень из семи целых двадцати девяти сотых». Слово «арифметический» произносят лишь тогда, когда хотят особо подчеркнуть, что речь идет именно о неотрицательном квадратном корне из числа.

В свете введенного обозначения из определения арифметического квадратного корня следует, что

для любого неотрицательного числа a.

Для отрицательных чисел a записи мы не будем придавать смысла вплоть до изучения комплексных чисел. Например, лишено смысла выражение:

$\sqrt{-4}$

На практике часто применяются свойства квадратных корней:

Cвойство квадратного корня из произведения двух неотрицательных действительных чисел a и b, задающееся равенством вида .

$\sqrt{a*b}=\sqrt{a}*\sqrt{b}}$

Корень из частного:

которое часто записывают с помощью дробей как:

$\sqrt{\frac{a}{b}}=\frac{\sqrt{}a}{\sqrt{b}}$

Свойство арифметического квадратного корня из степени числа a с четным показателем:

$\sqrt{a^{2m}}=|a^{m}|$

при любом действительном a, в частности, свойство квадратного корня из квадрата числа:

$\sqrt{a^{2}}=|a|$

Как вы уже заметили, корень — это та же степень. И, зная свойства степени, можно работать с корнем. Для корня рассмотрим еще такие свойства:

$n\sqrt{a^{m}}=a^{\frac{m}{n}},a\ge 0$

Сравнение чисел

Помимо заданий на извлечение корней, возведение выражений в степень, могут встретиться задания, в которых нужно расставить числа в порядке возрастания или убывания; указать наибольшее или наименьшее число, то есть сравнить.

Сравнивать можем целые числа, дробные числа, выражения, содержащие корни и степени. Рассмотрим несколько примеров.

Пример 1.

Значение какого из данных выражений является наибольшим? В ответе укажите номер правильного варианта.

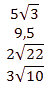
Сравнение чисел огэ

Решение.

Возведем каждое число в квадрат и сравним квадраты этих чисел:

Поскольку

75< 88<90<90,25

то наибольшим является выражение под номером 2.

Ответ: 2.

Пример 2.

Расстояние от Нептуна — одной из планет Солнечной системы — до Солнца равно 4450 млн. км. Как эта величина записывается в стандартном виде?

В ответе укажите номер правильного варианта.

4,450·10⁶ км

4,450·10⁷ км

4,450·10⁸ км

4,450·10⁹ км

Решение.

Для решения задач этого типа нужно вспомнить стандартный вид числа.

Число, записанное в стандартном виде, имеет вид:

Преобразуем число к стандартному виду:

Ответ: 4.

Пример 3.

Значение, какого из выражений является числом иррациональным?

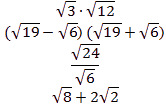
Примеры огэ математика

Для решения задач этого типа нужно вспомнить определения.

Рациональные числа — это числа, которые можно представить в виде дроби с целым числителем и натуральным знаменателем, есть, где m — целое, а n — натуральное.

Рациональные числа могут быть представлены конечным или бесконечным десятичным периодическим дробью. Множество рациональных чисел обозначается большой латинской буквой Q.

Иррациональными называются числа, которые нельзя представить в виде дроби, где m — целое, а n — натуральное. Иррациональные числа могут быть представлены бесконечными непериодическими дробями.

Решение.

1) Воспользуемся вынесением множителя из-под знака корня:

Таким образом, получили рациональное число.

2) Воспользуемся формулой сокращенного умножения:

Получили рациональное число.

3) Воспользуемся свойством извлечения корня из дроби:

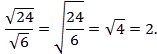
Примеры огэ математика

Получили рациональное число.

4) Вынесем множитель из-под знака корня:

Получили иррациональное число.

Ответ: 4.

Пример 4.

Сравните числа:

$\sqrt{67}+\sqrt{61} и 16$

В ответе укажите номер правильного варианта.

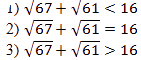
Примеры огэ математика

Решение.

Возведем каждое из чисел в квадрат. Получим:

Предположим, что квадраты данных чисел (а, значит и сами числа) равны. (Можно предположить, что первое число меньше второго или наоборот больше). Получим в результате преобразования:

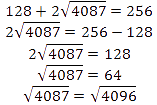
Примеры огэ математика

Данное равенство неверное

$\sqrt{4087} <\sqrt{4096}$

Следовательно

$\sqrt{67}+ \sqrt{61}< \sqrt{16}$

Ответ: 1.

Прототипы заданий 7 и 8 ОГЭ математика 2024

Задание 1

Найдите значения выражения:

$-80+0,3*(-10)^{3}$

Задание 2

Найдите значение выражения:

$0,8*(-10)^{2}-95$

Задание 3

Найдите значение выражения:

$2\sqrt{31}*3\sqrt{3}*\sqrt{93}$

Задание 4

Представьте выражение

$\frac{1}{x^{5}}*\frac{1}{x^{9}}$

в виде степени с основанием x. В ответе укажите номер правильного варианта:

1)x ¹⁴

2)x ⁵⁴

3)x ^-45

4)x ^-14

Задание 5

Какое из данных чисел является иррациональным?

$1)\sqrt{0.16}$

$2)\sqrt{1.6}$

$3)\sqrt{1600}$

4)все эти числа рациональны

Ответы к заданиям:

-380.
-15.
558.
4.
2.

Ответы на часто задаваемые вопросы

Что такое возведение в степень из ОГЭ?

Возведение в степень — это нахождение значения степени числа.

Что такое рациональные числа – разбор 8 задания ОГЭ?

Рациональные числа — это числа, которые можно представить в виде дроби с целым числителем и натуральным знаменателем, есть, где m — целое, а n — натуральное. Рациональные числа могут быть представлены конечным или бесконечным десятичным периодическим дробью. Множество рациональных чисел обозначается большой латинской буквой Q.

Что представляют собой иррациональные числа – ОГЭ по математике?

Иррациональными называются числа, которые нельзя представить в виде дроби, где m — целое, а n — натуральное. Иррациональные числа могут быть представлены бесконечными непериодическими дробями.

Все статьи