8bit > Математика ОГЭ > 21 задание ОГЭ по математике

21 задание ОГЭ по математике

11-05-2023

Дополнительные темы

Демоверсия ОГЭ по математике 2024 года 16 задание ОГЭ по математике – окружность, круг и их элементы 15 задание ОГЭ по математике – треугольники Практико-ориентированные задачи ОГЭ по математике 14 задание ОГЭ по математике Теория вероятностей в ОГЭ по математике 9 класс 21 задание ОГЭ по математике 20 задание ОГЭ по математике 12 задание ОГЭ по математике – расчеты по формулам Функции арифметического квадратного корня — ОГЭ по математике 11 задание ОГЭ по математике 13 задание ОГЭ по математике Рациональные уравнения ОГЭ 9 задание ОГЭ по математике 7 и 8 задания ОГЭ по математике 6 задание ОГЭ по математике Демоверсия ОГЭ по математике 2023 года

Как оформлять 21 задание ОГЭ по математике

Для того чтобы получить полный балл за решение 21 задачи, следует математически грамотно и полно раскрыть ответ – из него должен быть понятен ваш ход рассуждений. Оформление должно соответствовать этим требованиям, а в остальном может быть произвольным, не обязательно оставлять подробные комментарии по решению задач.

Задачи на движение – 21 задание ОГЭ по математике

1) Основная формула

S=v⋅t или путь = скорость × время

2) Относительное движение:

это сумма скоростей, если тела движутся навстречу друг другу;
это разность скоростей, если тела движутся в одном направлении.

3) Движение с течением:

если движемся по течению, к нашей скорости прибавляется скорость течения;
если движемся против течения, из скорости вычитается скорость течения.

Алгоритм решения 21 задания на движение – ОГЭ по математике

Он состоит из 2 больших этапов.

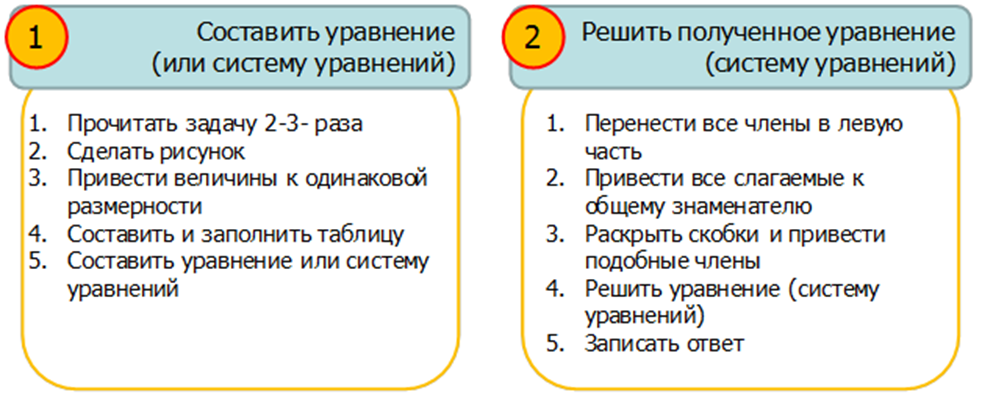
решения 21 задания на движение огэ
Но не забываем, что, если в уравнении в знаменателе есть переменная, то обязательно надо найти ОДЗ.

Разберем немного подробнее некоторые особенности и тонкости, возникающие при решении задач на движение.

Немного о внимательности в прочтении задач

Прочитать задачу нужно несколько раз. Необходимо осознать её настолько, чтобы было понятно абсолютно всё.

Например, часто возникают трудности с понятием «собственная скорость» лодки/катера и т.д. Что это может значить? Конечно, скорость лодки в стоячей воде, например, в пруду, когда на неё не влияет скорость течения. Кстати, в задачах иногда пишут «найти скорость лодки в стоячей воде». Таким образом, собственная скорость лодки и скорость лодки в стоячей воде — одно и то же.

Особенности задач на движение: кто куда едет, кто к кому приехал, и где они все встретились.

Лучше для себя на черновике сделать рисунок, попутно записывая на нём все известные величины (или под ним, если есть затруднения, как их отобразить схематически). Рисунок должен чётко отражать весь смысл задачи. Чертёж следует сделать таким образом, чтобы на нём была видна динамика движения — направления движения, встречи, развороты, повороты. Качественный чертеж позволяет понять задачу, не заглядывая в её текст. Он — основная подсказка для дальнейшего составления уравнения.

Рассмотрим возможные виды движения двух тел.

Движение навстречу друг другу

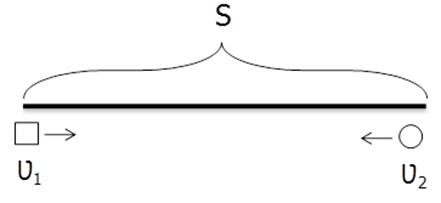
Если тела движутся навстречу друг другу, то их скорость сближения равна сумме их скоростей:

$v_{сближ}=v_{1}+v_{2}$

Когда тела одновременно выезжают навстречу друг другу и встречаются в какой-то точке, время их движения одинаково, тогда можно вычислить расстояние между точками старта:

$V_{1}t+V_{2}t=S\to (V_{1}+V_{2})t=S$

Отсюда и появилась скорость сближения.

Пример

Пусть из точки А и из точки В навстречу друг другу выехали две машины. Скорость одной машины — 60 км/ч, а скорость второй машины — 40 км/ч. Они встретились через 1,2 часа. Какое расстояние между пунктами А и В?

1 вариант решения

60 *1,2=72 (км) — путь, который проехала первая машина.
40*1,2=48(км) — путь, который проехала вторая машина.
72+48=120(км) — расстояние между пунктами.

2 вариант решения (более рациональный, но оба решения являются верными)

60 + 40 = 100 (км/ч) — скорость сближения.
1,2 * 100 = 120 (км) — расстояние между пунктами.

Примечание. Если первоначальное расстояние между телами равно S, то время, через которое они встретятся, вычисляется по формуле:

$t_{встр}=\frac{S}{v_{1}+v_{2}}$

Движение в противоположные стороны

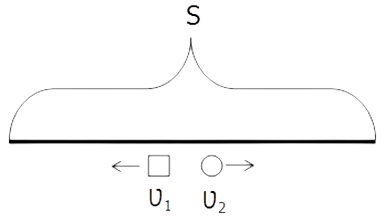
Если тела удаляются друг от друга, то их скорость удаления равна сумме их скоростей:

$v_{удал}=v_{1}+v_{2}$

Доказать аналогично первому случаю.

Пример

Из Москвы в противоположные стороны выехало две машины. Скорость одной машины — 85 км/ч, скорость другой — 60 км/ч. На каком расстоянии друг от друга будут находиться машины через 2 часа?

1 вариант решения

85 * 2 = 150 (км) — путь, который проехала первая машина.
60 * 2 = 120 (км) — путь, который проехала вторая машина.
170 + 120 = 290 (км) – расстояние между пунктами.

2 вариант решения (более рациональный, но оба решения являются верными)

85 + 60 = 145 (км/ч) – скорость удаления.
145 * 2 = 290 (км) – расстояние между пунктами.

Примечание. Время, проведенное телами в пути, при удалении друг от друга равно пройденному расстоянию (то есть, если между телами изначально было некое расстояние S_o, то его следует вычесть из общего расстояния), деленному на сумму скоростей тел:

$t_{пути}=\frac{S}{v_{1}+v_{2}}$

А что, если тела изначально находятся на некотором расстоянии друг от друга? Это выглядит примерно так:

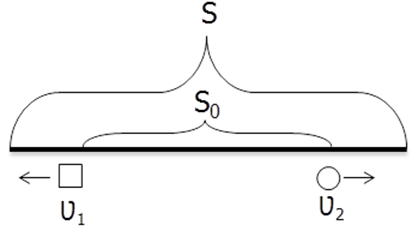
огэ математика

Как решать подобные задачи тогда? Очень просто. При решении нам необходимо обязательно учитывать S_o.

Если существует какое-либо первоначальное расстояние между телами, то формула пути выглядит следующим образом:

$S=S_{0}+(v_{1}+v_{2})*t$

Выразим время, получим:

$t=\frac{S-S_{0}}{v_{1}+v_{2}}%$

Движение в одном направлении

Пусть два тела двигаются в одном направлении. Возникает вопрос, сколько случаев может быть для такого условия? Конечно, два.

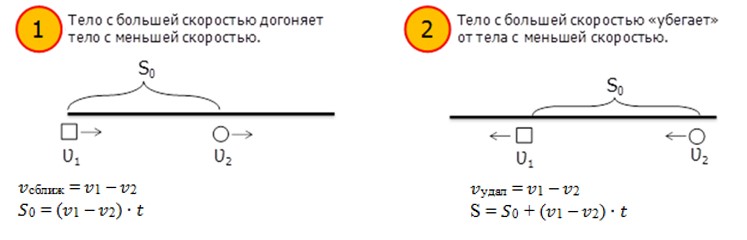
Движение в одном направлении огэ

Пример

Коля едет на работу на машине со скоростью 60 км/ч. Коллега Коли Вова едет со скоростью 85 км/ч. Коля от Вовы живет на расстоянии 15 км. Через сколько времени Вова догонит Колю, если из дома они выехали одновременно?

Решение

85 – 60 = 25 (км/ч) — скорость сближения.
15 : 25 = 0,6 (часа) — через столько времени Вова догонит Колю.

Ответ: через 0,6 часа или 36 минут.

Онлайн подготовка к ЕГЭ и ОГЭ 2025 с выгодой до 30%

Занятия в мини-группах с экспертами ЕГЭ по всем школьным предметам

Узнать подробнее

Размерность – разбор 21 задания ОГЭ математика

Далеко не всегда в задачах дается одинаковая размерность для каждого участника движения. Например, можно встретить задачи, где сказано, что тела двигались определенное количество минут, а скорость их передвижения указана в км/ч. Мы не можем просто взять и подставить значения в формулу — ответ получится неверный. Даже по единицам измерения наш ответ «не пройдет» проверку на разумность. Обратите внимание:

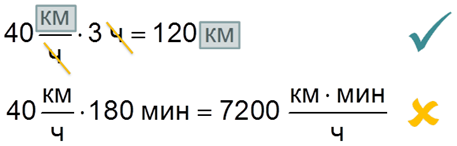
разбор 21 задания огэ по математике 2023

При грамотном перемножении сокращаются единицы измерения, и, соответственно, получается разумный и верный результат. А что происходит, если не переводить в одну систему измерения? Странная размерность у ответа и 100% неверный результат.
Вспомним значения основных единиц измерения длины и времени.

Единицы измерения длины:

1 сантиметр = 10 миллиметров
1 дециметр = 10 сантиметров = 100 миллиметров
1 метр = 10 дециметров = 100 сантиметров = 1000 миллиметров
1 километр = 1000 метров

Единицы измерения времени:

1 минута = 60 секунд
1 час = 60 минут = 3600 секунд
1 сутки = 24 часа = 1440 минут = 86400 секунд

А теперь рассмотрим более сложную задачу на движение, для решения которой лучше всего не просто нарисовать рисунок, но и составить таблицу со всеми данными условия.

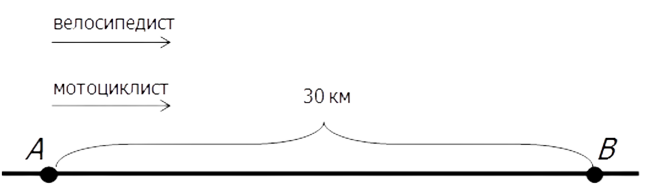
Задача

Из пункта A в пункт B, расстояние между которыми 30 км, одновременно выехал велосипедист и мотоциклист. Известно, что в час мотоциклист проезжает на 65 км больше, чем велосипедист. Определите скорость велосипедиста, если известно, что он прибыл в пункт B на 156 минут позже, чем мотоциклист.

Решение

1) Сделаем рисунок.

прототипы задания 21 огэ математика

2) Рисуем таблицу. Все задачи на движения состоят из 3 компонентов: скорость, время и путь. Именно из этих граф и будет состоять любая таблица в подобных задачах. Но можно добавить еще один столбец — имя, название и т.д., то есть то, про кого идет речь в задаче. В данном случае мотоциклист и велосипедист. Также в шапке укажем размерность, в какой будем вписывать туда величины. Итак, рисуем таблицу и заполняем её.

	Скорость , км\ч	Время , ч	Путь , км
Велосипедист
Мотоциклист

Первое, что мы имеем — это путь, который проделали велосипедист и мотоциклист. Он одинаков и равен 30 км. Вносим в таблицу!

	Скорость , км\ч	Время , ч	Путь , км
Велосипедист			30
Мотоциклист			30

Рассуждаем дальше. Мы знаем, что мотоциклист проезжает на 65 км/ч больше, чем велосипедист, да и в задаче нужно найти скорость велосипедиста. Возьмем скорость велосипедиста за x, тогда скорость мотоциклиста будет x+65.

	Скорость , км\ч	Время , ч	Путь , км
Велосипедист			30
Мотоциклист			30

Осталось заполнить только одну графу — время. Чтобы найти время, надо разделить путь на скорость. Вносим это в таблицу.

	Скорость , км\ч	Время , ч	Путь , км
Велосипедист			30
Мотоциклист			30

Теперь можно внести данные на рисунок.

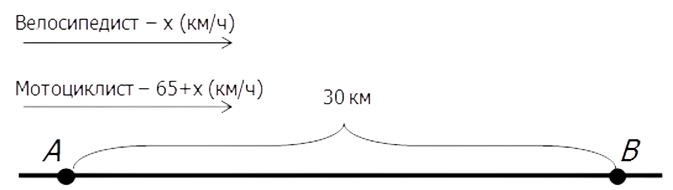
Огэ математика

Еще раз перечитаем задачу, посмотрим на рисунок и заполненную таблицу. Видно, что не отражено ни в таблице, ни на рисунке время, на которое мотоциклист приехал раньше, чем велосипедист. Мы знаем, что разница во времени — 156 минут. переводим данное время из минут в часы, ведь скорость дана в км/ч.

156 минут=2,6 часа.

А теперь составляем и решаем уравнение. Мы из времени медленного будем вычитать время быстрого, быстрый — у кого скорость больше, а значит, время движения меньше, и наоборот. Данный анализ позволяет не путаться в составлении уравнения.

$\frac{30}{x}-\frac{30}{x+65}=2,6$

$\frac{30}{x}-\frac{30}{x+65} -2,6 =0$

Приводим к общему знаменателю. Получим:

$\frac{30x+1950-30x-2,6x^{2}-169x}{x(x+65)}=0$

$\frac{1950-2,6x^{2}-169x}{x(x+65)}=0$

$\frac{x^{2}+65x-750}{x(x+65)}=0$

Найдем ОДЗ:

$x(x+65)\neq 0$

$x\neq 0,x\neq-65$

Найдем корни уравнения:

$x^{2}-65x-750=0$

$x_{1}=10,x_{2}=-75$

Оба числа удовлетворяют ОДЗ, но, так как скорость не может быть отрицательной, то подходит число 10. Это и есть скорость велосипедиста, которую принимали за x.

Ответ: 10 км/ч.

Подобное уравнение составляется в случаях, когда кто-то из объектов сделал остановку и в итоге прибыл со вторым одновременно, так как время, затраченное на его движение меньше, чем у того, кто не останавливался. Также в случае, когда один стартовал на какое-то время позже второго и прибыл одновременно с другим в пункт назначения.

Задачи на течение – 21 задание ОГЭ по математике теория и практика

Нужно обратить внимание:

21 задание ОГЭ по математике

Рассмотрим для примера следующую задачу. При решении можно рисовать рисунок или таблицу. Это на ваше усмотрение.

Задача

Расстояние между пристанями А и В равно 90 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 52 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 4 км/ч.

Решение

Пока лодка шла из точки A в точку B и обратно, плот по течению реки проплыл 52 км. Учитывая скорость течения реки 4 км/ч, получаем время движения плота 52 : 4 = 13 часов. Так как лодка отправилась вслед за ним только через час, то ее время в пути будет равно 13 – 1 = 12 часов. Обозначим теперь через x км/ч собственную скорость лодки. Из пункта A в B она шла по течению, то есть со скоростью x+4 км/ч и путь в 90 км составил 90/(x+4) часов. Обратно она шла против течения и тот же путь проделала за 90/(x-4) часа. Все время пути равно 12 часов. Так как мы знаем общее время движения по течению и против, то время можно сложить. Получаем уравнение:

$\frac{90}{x+4} +\frac{90}{x-4}=12$

ОДЗ: x≠4,x≠4.

упрощаем, имеем:

$90*(x_{4})+90*(x+4)-12*(x^{2}-16)=0$

$-12x^{2}+180x+192=0$

$x^{2}-15x-16=0$

$x_{1}=16,x_{2}=-2,5$

Так как собственная скорость лодки не может быть отрицательной величиной, получаем значение 16 км/ч.

Ответ: 16 км/ч.

Довольно часто попадаются задачи на нахождение средней скорости на протяжении всего пути. Чтобы найти среднюю скорость на каком-то пути, нужно весь этот путь разделить на всё время движения по пути:

$v_{ер}=\frac{S_{полный}}{t_{полное}}$

Задача

Автомобиль 2 часа ехал со скоростью 50 км/ч, потом час со скоростью 100 км/ч, далее 2 часа со скоростью 75 км/ч. Найдите среднюю скорость автомобиля.

Решение строго по формуле вычисляем

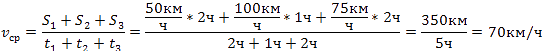
Огэ математика формулы

Очень часто требуется найти среднюю скорость автомобиля, который ехал с разной скоростью равные промежутки времени или равные дистанции. В таком случае обозначаем за t или S ту неизвестную, которая «сохраняется».

Задача

Первую половину времени автомобиль ехал со скоростью v₁, вторую половину времени со скоростью v₂. Найдите среднюю скорость движения автомобиля (пусть общее время движения равно t).

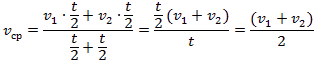
21 задание ОГЭ по математике портотипы

Аналогичные уравнения можно составить для трех, четырех, главное, равных промежутков времени.

Мораль: если автомобиль едет равные промежутки времени, средняя скорость равна среднему арифметическому скоростей на равных по времени участках.
Посмотрим опять первый пример. Его можно было бы теперь решить иначе: скажем, что автомобиль едет 5 равных промежутков времени со скоростями 50, 50, 100, 75 и 75 км/ч. Сложив все и разделив на 5, получим ответ.

Равные дистанции, равные промежутки пути

Первую половину пути автомобиль двигался со скоростью v₁, вторую половину пути — со скоростью v₂. Найдите среднюю скорость движения.
Так как в задаче написано только про скорость и путь, то обозначим путь как S.

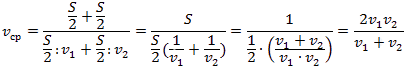
Огэ математика

Относительная скорость – ОГЭ математика текстовые задачи

При решении подобных задач нужно задать себе пять вопросов:

Кого столбим, обездвиживаем?
Относительная скорость — вычитаем или складываем?
Чему равен путь?
Чему равно время?
Все ли в порядке с единицами измерения или нужно переводить?

Составить уравнение движения вида:

$S=v_{отн}*t$

Прототипы 21 задания ОГЭ по математике 2024

Задача 1

Из пункта А в пункт В, расстояние между которыми 13 км, вышел пешеход. Одновременно с ним из В в А выехал велосипедист. Велосипедист ехал со скоростью, на 11 км/ч большей скорости пешехода, и сделал в пути получасовую остановку. Найдите скорость пешехода, если известно, что они встретились в 8 км от пункта В.

Задача 2

Из пункта А в пункт В, расстояние между которыми 27 км, вышел турист. Через полчаса навстречу ему из пункта В вышел пешеход и встретил туриста в 12 км от А. Найдите скорость туриста, если известно, что она была на 2 км/ч меньше скорости пешехода.

Задача 3

Из пункта А в пункт В, расстояние между которыми 19 км, вышел пешеход. Через полчаса навстречу ему из пункта В вышел турист и встретил пешехода в 9 км от В. Турист шёл со скоростью, на 1 км/ч большей, чем пешеход. Найдите скорость пешехода, шедшего из А.

Задача 4

Два велосипедиста одновременно отправляются в 180-километровый пробег. Первый едет со скоростью на 5 км/ч большей, чем второй, и прибывает к финишу на 3 часа раньше второго. Найдите скорость велосипедиста, пришедшего к финишу первым.

Ответы к заданиям

Ответ: 5.
Ответ: 4.
Ответ: 5.
Ответ: 20.

Ответы на часто задаваемые вопросы

Какие типы задач встречаются в задании 21 ОГЭ по математике?

Движение навстречу друг другу, движение в противоположные стороны, движение параллельно с разными скоростями, движение по течению.

На что обратить внимание при решении задач на движение?

Особенности задач на движение: кто куда едет, кто к кому приехал и где они все встретились.

Как рассчитать скорость лодки в стоячей воде, если известна собственная скорость лодки?

В водоеме вода стоячая, когда в нем отсутствует течение. То есть когда объект движется в стоячей воде, это и считается его собственной скоростью.

Все статьи