















20 задание ОГЭ по математике
Краткий ответ, к ак решать задания на неравенства из ОГЭ по математике
Для того чтобы научиться решать задания экзамена ОГЭ, где встречаются линейные неравенства и их системы, следует основательно знать теорию. А именно – основные понятия, обозначения и правила преобразования неравенств.
Задание 20 ОГЭ математика линейные неравенства – теория
Линейными неравенствами называются неравенства вида:
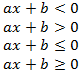
где a и b — любые числа, причем a≠0, x – неизвестная переменная.
Обозначения на координатной прямой и в записи ответа в виде множества:
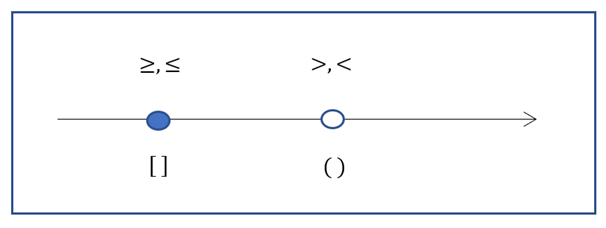
Сводная таблица числовых промежутков
Правила преобразования неравенств – задание 20 ОГЭ математика
Правило 1. Любой член неравенства можно переносить из одной части неравенства в другую, меняя при этом знак на противоположный (т.е. при переносе через знак неравенства знаки при слагаемых меняются на противоположные, как в уравнении).
Правило 2. Обе части неравенства можно умножить/разделить на одно и то же положительное число, при этом получится неравенство, равносильное данному.
Правило 3. Обе части неравенства можно умножить/разделить на одно и то же отрицательное число, меняя знак неравенства на противоположный (т.е. знак > на знак < и наоборот; знак ≥ на знак ≤ и наоборот).
Пример
Укажите решение неравенства:
![]()
Решение
Для решения линейного неравенства достаточно выполнить действия, аналогичные действию решений линейных уравнений. Однако, в отличие от линейных уравнений, следует проявлять внимательность при выполнении операций деления или умножения на отрицательное число — в этих случаях знак неравенства будет меняться на противоположный!
Для решения этого примера вначале раскроем скобки, не забывая, что -3 умножается на -7 и дает +27:
![]()
Затем приводим подобные, перенося числа в правую сторону:
![]()
Нам необходимо умножить неравенство на -1, чтобы получить диапазон x, не забывая, что при этом меняется знак неравенства:
![]()
Таким образом, мы получаем, что x должен быть больше либо равен 18.
Ответ:
![]()




- Как поступить в любой вуз по олимпиаде в 2026 году.
- Бесплатный курс ЕГЭ по математике 2026 (профиль)
- Бесплатный курс ЕГЭ по русскому языку 2026
- Бесплатный курс ОГЭ по математике 2026
- 10 главных правил: Как сдать ЕГЭ на 80+ баллов


Разбор 20 задания ОГЭ по математике
Квадратное неравенство — это неравенство вида:
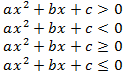
где a, b, c – числа, x≠0, x – переменная.
Для решения квадратного неравенства используется специальный способ, который называется методом интервалов.
Чтобы решить квадратное неравенство методом интервалов, нужно:
- Перенести все члены неравенства в левую часть так, чтобы в правой остался только нуль.
- Сделать так, чтобы при неизвестном «x2» стоял положительный коэффициент.
- Приравнять левую часть неравенства к нулю и решить полученное квадратное уравнение.
- Записать разложенное на множители выражение по формуле a(x-x1)(x-x2) . Полученные корни уравнения разместить на числовой оси в порядке возрастания.
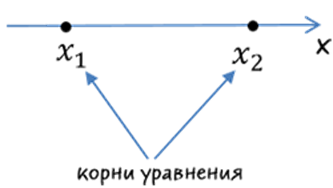
- Нарисовать «арки» для интервалов. Справа налево, начиная с «+», проставить, чередуя знаки «+» и «−».
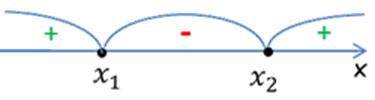
- Выбрать необходимые интервалы и записать их в ответ.
Пример
Требуется решить квадратное неравенство: x2 +x-12 <0
Итак, согласно пункту 1 мы должны перенести все члены неравенства в левую часть, так чтобы в правой части остался только нуль. В заданном неравенстве ничего дополнительно делать не требуется, так как в правой части и так уже стоит нуль.
Переходим к пункту 2. Необходимо сделать так, чтобы перед «x2 » стоял положительный коэффициент. В неравенстве x2 +x-12 <0 при «x2» стоит положительный коэффициент «1», значит, снова нам ничего делать не требуется.
Согласно пункту 3 приравняем левую часть неравенства к нулю и решим полученное квадратное уравнение:
x2 +x-12 =0
Получим корни уравнения:
x1=4, x2=-3
(x-4)(x+3)<0
Теперь согласно пункту 4 отметим полученные корни на числовой оси в порядке возрастания.

Необходимо помнить, что, исходя их того, какое перед нами неравенство (строгое или нестрогое) мы отмечаем точки на числовой оси соответствующим способом.
Теперь, как сказано в пункте 5, нарисуем «арки» над интервалами между отмеченными точками.

Проставим знаки внутри интервалов. Справа налево, чередуя, начиная с «+», отметим знаки.
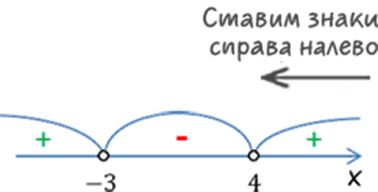
Нам осталось только выполнить пункт 6, то есть выбрать нужные интервалы и записать их в ответ. Вернемся к нашему неравенству.
Так как в нашем неравенстве знак неравенства < значит, нам требуются отрицательные интервалы. Заштрихуем все отрицательные области на числовой оси и выпишем их в ответ.

Отрицательным интервалом оказался лишь один, который находится между числами «−3» и «4», поэтому запишем его в ответ в виде двойного неравенства -3<x<4.
Ответ: -3<x<4
Решение 20 задания ОГЭ по математике — системы неравенств
Система неравенств состоит из нескольких неравенств с одной переменной. Эти неравенства объединяются фигурной скобкой (так же, как и уравнения в системах уравнений).
Задача состоит в том, чтобы найти все общие решения заданных неравенств.
Значение переменной, при котором каждое из неравенств системы становится верным числовым неравенством, называют решением системы неравенств.
Множество всех решений системы неравенств является общим решением (чаще всего — просто решением системы неравенств.)
Решить систему неравенств — это найти все её решения. Чтобы решить систему неравенств нужно:
- решить отдельно каждое неравенство;
- сравнить полученные решения каждого неравенства и получить общий ответ системы.
Пример
Укажите множество системы неравенств:
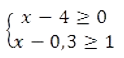
Решение
Решение системы линейных неравенств сводится к решению линейного неравенства с дальнейшим анализом промежутков. В начале действуем аналогично первому случаю: переносим числа в правую часть, оставляя x слева:
![]()
Сравним промежутки и выберем общий. Первое неравенство требует, чтобы x был больше 4, а второе — более 1,3. На координатной прямой это будет выглядеть следующим образом:
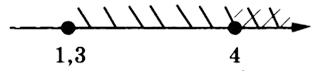
Промежутки перекрывают друг друга, начиная с 4. Значит, ответ выглядит следующим образом (не забываем, что неравенство нестрогое): [4;+∞ ] или
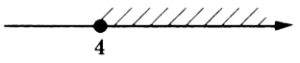
Пример
Решите систему неравенств:
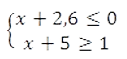
На каком рисунке изображено множество ее решений?
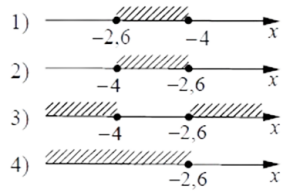
Решение
Итак, решим систему неравенств — оставим x в левой части, а остальное перенесем в правую, получим:
![]()
Вычислив, получаем ответ:
![]()
Найдем его на координатной прямой. Это №2.
Ответ: 2.
 Прототипы задания 20 ОГЭ по математике 2024 года
Прототипы задания 20 ОГЭ по математике 2024 года
Задание 1
Решите систему неравенств
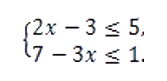
Задание 2
Найдите наименьшее значение x , удовлетворяющее системе неравенств
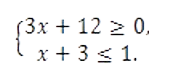
Задание 3
Решите систему неравенств
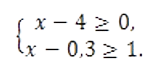
Задание 4
Найдите наименьшее значение x, удовлетворяющее системе неравенств
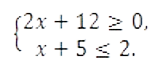
Задание 5
Найдите наибольшее значение x, удовлетворяющее системе неравенств
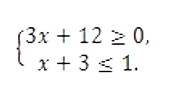
Задание 6
Решите систему неравенств
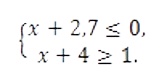
Ответы к заданиям
- Ответ: 2;4 .
- Ответ: -4.
- Ответ: 4;+∞ .
- Ответ: -6.
- Ответ: -2.
- Ответ: -3;-2,7 .
Ответы на часто задаваемые вопросы

Что включает 6 задание ОГЭ? Числа на прямой и числовые неравенства – одна из первых тем, с которой нужно ознакомиться для успешного решения заданий экзамена. Речь идет об арифметических операциях…

Что представляет собой 11 задание ОГЭ по математике 2024? В 11 задании ОГЭ по математике 2024 идет работа с графиками функций. В большинстве случаев требуется установить соответствие между графиком функции…
