8bit > Математика ОГЭ > 16 задание ОГЭ по математике – окружность, круг и их элементы

16 задание ОГЭ по математике – окружность, круг и их элементы

22-05-2023

Дополнительные темы

Демоверсия ОГЭ по математике 2024 года 16 задание ОГЭ по математике – окружность, круг и их элементы 15 задание ОГЭ по математике – треугольники Практико-ориентированные задачи ОГЭ по математике 14 задание ОГЭ по математике Теория вероятностей в ОГЭ по математике 9 класс 21 задание ОГЭ по математике 20 задание ОГЭ по математике 12 задание ОГЭ по математике – расчеты по формулам Функции арифметического квадратного корня — ОГЭ по математике 11 задание ОГЭ по математике 13 задание ОГЭ по математике Рациональные уравнения ОГЭ 9 задание ОГЭ по математике 7 и 8 задания ОГЭ по математике 6 задание ОГЭ по математике Демоверсия ОГЭ по математике 2023 года

Как решать 16 задание ОГЭ по математике

Для этого потребуется повторить определения окружности и круга, их свойства, а также вспомнить формулы, которые встречаются в задачах 16. Научившись применять свойства и рассчитывать углы по формулам, вы сможете находить правильный ответ к заданиям любой сложности.

Окружность, круг, их элементы – задание 16 ОГЭ математика 2024

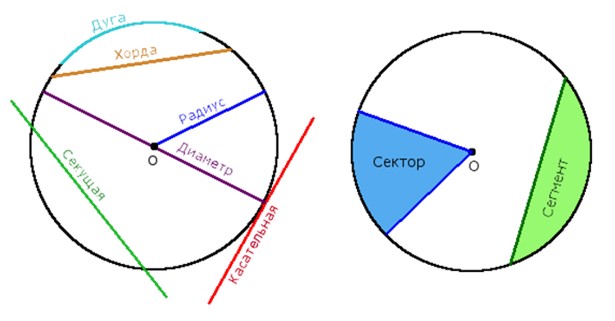
задание 16 ОГЭ математика 2023

Окружность — это плоская замкнутая кривая, все точки которой находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.

Круг — часть плоскости, ограниченная окружностью.

Радиус окружности R — расстояние от центра окружности О до любой точки окружности.

Диаметр окружности D — отрезок, который соединяет две точки окружности и проходит через ее центр.

Основные свойства окружности

Диаметр окружности равен двум радиусам:D=2r
Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса. (Поэтому радиус, проведенный в точку касания перпендикулярен касательной).

Формулы длины окружности и площади круга

Формулы длины окружности:

Формула длины окружности через диаметр: L=πD
Формула длины окружности через радиус: L=2πr

Формулы площади круга:

Формула площади круга через радиус: S=πr²
Формула площади круга через диаметр:

$S=\frac{\pi D^{2}}{4}$

Касательная, секущая, хорда окружности – 16 задание ОГЭ по математике

Касательная окружности — прямая, которая касается окружности только в одной точке.

Основные свойства касательных к окружности:

Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения и наоборот.
Кратчайшее расстояние от центра окружности к касательной равно радиусу окружности.

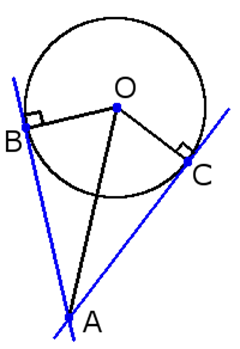
окружности 16 задание ОГЭ по математике

Отрезки касательных, заключенные между точкой пересечения касательных и точками касания с окружностью, равны:

AB=AC

Углы, заключенные между касательными и прямой, проходящей через центр окружности и точку пересечения касательных, равны:

∠ OAC= ∠ OAB

Секущая окружности — прямая, которая проходит через две точки окружности. На рисунке секущая KN.

Хорда окружности — отрезок, который соединяет две точки окружности. На рисунке хорда AB.

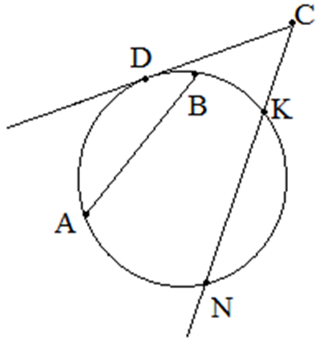
окружности 16 задание ОГЭ по математике

Свойство секущей и касательной: Если из точки, лежащей вне окружности, проведены касательная и секущая, то квадрат длины отрезка касательной равен произведению отрезков секущей:

$CD^{2}=CK*CN$

Хорда окружности обладает следующими свойствами:

Хорды, находящиеся на одинаковом расстоянии от центра окружности, равны.
Если диаметр перпендикулярен хорде, то он проходит через ее середину.
Две дуги равны, если они заключены между двумя равными хордами.

Центральный угол, вписанный угол и их свойства – задание 16 ОГЭ математика 9 класс 2024

Центральный угол окружности — угол, вершиной которого есть центр окружности.

Угол, вписанный в окружность — угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.

Основные свойства углов:

Все вписанные углы, которые опираются на одну дугу — равны.

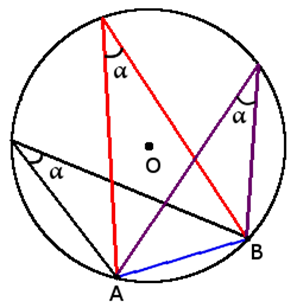
Основные свойства углов

Вписанный угол, который опирается на диаметр, будет прямым (90°).

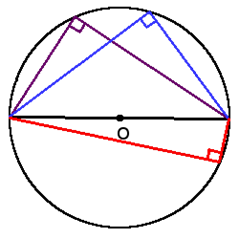
Основные свойства углов

Вписанный угол равен половине центрального угла, что опирается на ту же дугу

Основные свойства углов огэ

Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.

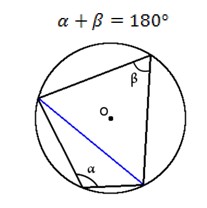
Основные свойства углов огэ

Дуга окружности — часть окружности, которая соединяет две точки на окружности.

Градусная мера дуги — угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.

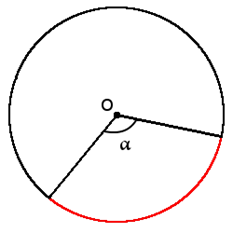
Градусная мера дуги огэ

Формула длины дуги через центральный угол (в градусах):

$l=\frac{\pi r}{180^{o}}*a$

Полуокружность — дуга, в которой концы соединены диаметром окружности.

Полукруг — часть круга, которая ограничена полуокружностью и диаметром.

Сектор — часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

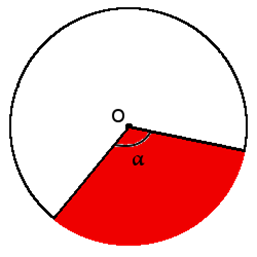
Градусная мера дуги огэ

Формула площади сектора через центральный угол (в градусах):

$l=\frac{\pi r^{2}}{180^{o}}*a$

Вписанная и описанная окружности – разбор 16 задания ОГЭ по математике 2024

Окружность вписана в n-угольник, если она касается всех сторон этого n-угольника.

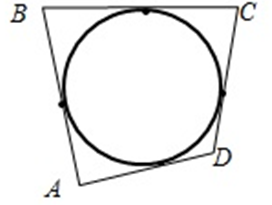
Вписанная и описанная окружности огэ

Окружность описана около n-угольника, если все вершины n-угольника лежат на окружности.

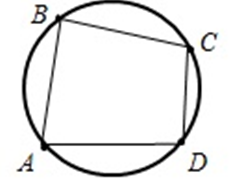
Вписанная и описанная окружности огэ математика

Свойства вписанной окружности:

Окружность можно вписать в любой треугольник.
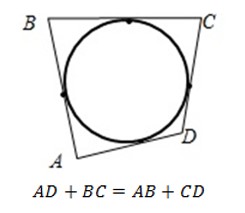
Окружность можно вписать в четырехугольник, если суммы длин его противолежащих сторон равны. Например, на рисунке:

Так, окружность можно вписать в квадрат и в ромб, но нельзя вписать в любой параллелограмм и в прямоугольник.

Вписанная и описанная окружности

Свойства описанной окружности:

Окружность можно описать около любого треугольника.
Окружность можно описать около четырехугольника, если суммы его противолежащих углов равны (180°). Например, на рисунке:

Так, окружность можно описать около квадрата и прямоугольника, но нельзя описать около любого параллелограмма и ромба.

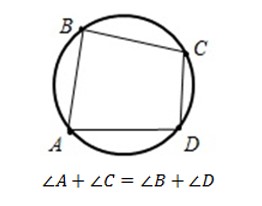
Вписанная и описанная окружности огэ 16 задание

Расположение центров окружностей, описанных около треугольника:

1) центр окружности расположен на пересечении серединных перпендикуляров к сторонам треугольника;

2) если треугольник остроугольный, то центр окружности расположен в этом треугольнике:

а) в равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника (центры вписанной и описанной окружностей совпадают;

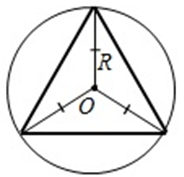
Расположение центров окружностей

б) в равнобедренном треугольнике центр окружности расположен на биссектрисе, проведенной из вершины треугольника к его основанию;

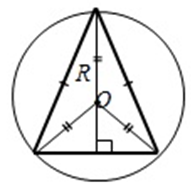
Расположение центров окружностей огэ

3) если треугольник прямоугольный, то центр окружности расположен на середине гипотенузы;

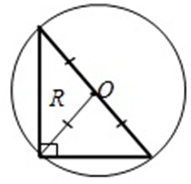
Расположение центров окружностей огэ

4) если треугольник тупоугольный, то центр окружности расположен вне треугольника.

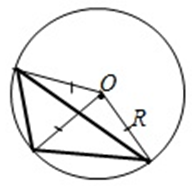
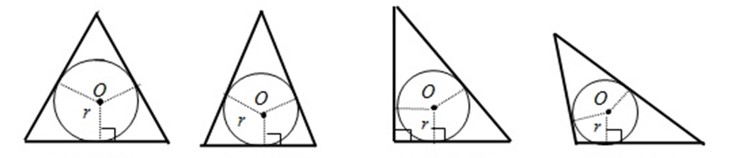
Расположение центров окружностей огэ

Расположение центров окружностей, вписанных в треугольник:

Центр окружности, вписанной в треугольник, расположен внутри треугольника;
Центром окружности является точка пересечения биссектрис треугольника;
В равностороннем треугольнике центром окружности является точка пересечения высот, биссектрис, медиан треугольника.

Расположение центров окружностей огэ

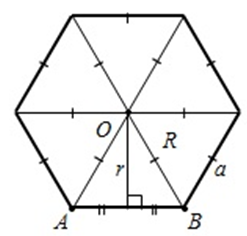
Правильный шестиугольник состоит из шести правильных треугольников, и точка является центром вписанной в него и описанной около него окружностей. И тогда сторона правильного шестиугольника равна радиусу описанной окружности.

16 задания ОГЭ по математике

Варианты 16 задания ОГЭ по математике

Задача 1

Найдите площадь кругового сектора, если длина ограничивающей его дуги равна 6π, угол сектора равен 120°, а радиус круга равен 9. В ответ укажите площадь, деленную на π.

Решение

Площадь сектора равна

$S=\frac{\pi*r^{2}}{360}*a$

имеем:

$S=\frac{\pi*81}{360}*120=27\pi$

Ответ: 27.

Задача 2

Прямая касается окружности в точке K. Точка O — центр окружности. Хорда образует с касательной угол, равный 83°. Найдите величину угла OMK. Ответ дайте в градусах.

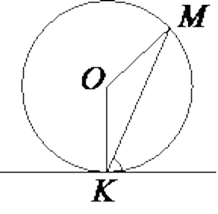
Варианты 16 задания ОГЭ по математике

Решение

Угол, образованный хордой и касательной, равен половине дуги, которую он заключает, поэтому величина дуги MK равна 2 · 83° = 166°. Угол MOK — центральный, поэтому он равен величине дуги, на которую опирается. Значит, угол MOK равен 166°.

В треугольнике OMK стороны OK и OM равны как радиусы окружности, поэтому треугольник OMK — равнобедренный, следовательно, углы при основании равны. Сумма углов треугольника равна 180°, поэтому ∠OKM = ∠ OMK = (180° − ∠ KOM ) / 2 = (180° − 166°) / 2 = 7°.

Ответ: 7.

Задача 3

Окружность с центром в точке O описана около равнобедренного треугольника ABC, в котором AB=BC и ∠ ABC = 177°. Найдите величину угла BOC. Ответ дайте в градусах.

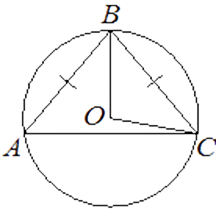
прототипы 16 задания ОГЭ по математике

Решение

Сумма углов треугольника равна 180°. Треугольник ABC — равнобедренный, следовательно

$\angle BAC =\angle BCA=\frac{180^{o }-177^{o}}{2}=1,5$

Угол BAC — вписанный, поэтому он равен половине дуги, на которую опирается. Угол BOC — центральный, поэтому он равен величине дуги, на которую опирается. Углы BAC и BOC опираются на одну и ту же дугу, следовательно

$\angle BOC =2 \angle BAC=3^{o}$

Ответ: 3.

Задача 4

Прямоугольный треугольник с катетами 5 см и 12 см вписан в окружность. Чему равен радиус этой окружности?

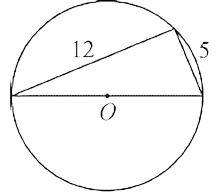
прототипы 16 задания ОГЭ по математике

Решение

Пусть R — радиус описанной окружности. Так как окружность описана вокруг прямоугольного треугольника, то ее центр лежит на середине гипотенузы. Таким образом, гипотенуза равна 2R.

$2R=\sqrt{144+25}=13$

$R=6,5$

По теореме Пифагора имеем:

Ответ: 6,5.

Задача 5

В угол C величиной 83° вписана окружность, которая касается сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.

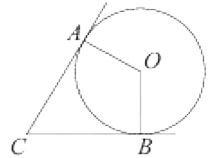
прототипы 16 задания ОГЭ по математике

Решение

Радиус окружности перпендикулярен касательной в точке касания, поэтому углы CAO и OBC равны 90°. Сумма углов четырёхугольника равна 360°, откуда:

∠AOB = 360° −∠CAO − ∠OBC − ∠ACB = 360° − 90° − 90° − 83° = 97°.

Ответ: 97.

Подготовьтесь к ЕГЭ или ОГЭ за 4 месяца

Интенсивный онлайн курс в Годографе с экспертами МЦКО

Узнать подробнее

Ответы на часто задаваемые вопросы

Что такое секущая окружности?

Секущая окружности — прямая, которая проходит через две точки окружности. На рисунке секущая KN.

Что такое хорда окружности?

Хорда окружности — отрезок, который соединяет две точки окружности. На рисунке хорда AB.

Чем отличаются вписанная и описанная окружности?

Окружность вписана в n-угольник, если она касается всех сторон этого n-угольника. Окружность описана около n-угольника, если все вершины n-угольника лежат на окружности.

Все статьи