
Курсы подготовки к ЕГЭ 2019 в Москве
Получите от +25 до +45 баллов к ЕГЭ по любому предмету
за 8 месяцев подготовки по уникальной методике экспертов ЕГЭ
Запишитесь на 2019/20 учебный год на самых выгодных условиях - от 5900 рублей в месяц
6 принципов, которые позволяют готовиться эффективнее, чем с репетитором!
Команда ТОП репетиторов по математике с опытом работы от 50 учеников!
Математика – один из сложнейших предметов ЕГЭ: всего 3% выпускников справляются с экзаменом на 80+ баллов.Благодаря тщательному многоступенчатому отбору нам удалось подобрать лучших преподавателей, которые просто и доступно объяснят даже вторую часть экзамена (с 13 по 19 задачу).
Вы научитесь понимать математику!
Подробнее о команде по математикеГрамотный старт
- Определяем начальный уровень выпускника.
- Ставим конкретную цель.
- Формируем личную систему достижений с учётом особенностей ученика.
- Прорабатываем формат распределения времени.
- Работаем с концентрацией.
Никаких лекций – максимальный упор на результат в баллах ЕГЭ, и ещё 7 проверенных правил, которые делают обучение в нашем центре эффективнее даже индивидуальных занятий!
Наши принципы:
- Проработка всех задач первой (1-12) и второй (13-19) части;
- Занятия по группам, сформированным в зависимости от начального уровня подготовки;
- Чёткое видение и понимание конечной цели;
- Работа над темой до тех пор, пока все ученики не научатся решать без ошибок.
Программа курса, учитывающая все актуальные требования ЕГЭ и одобренная Департаментом образования
- Методическая программа нашего центра;
- Циклическое повторение материала в течение всего обучения;
- Методика работы над формальными деталями экзамена.
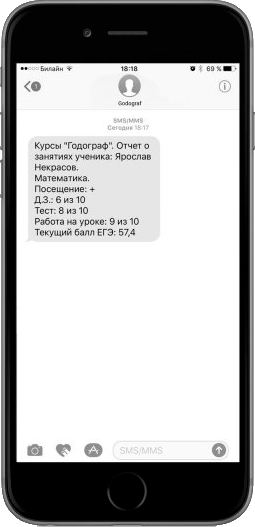
Поддержка 24/7. Регулярный полный контроль прогресса учеников, измеряемый в баллах ЕГЭ!
- Постоянная связь с преподавателем группы и поддержка ученика;
- 3 полноценных теста в формате ЕГЭ в течение всего учебного года;
- Проверка усвоения материала после каждого занятия и прогнозирование результата в баллах ЕГЭ;
- Отчёт включает результаты по 6 различным критериям.
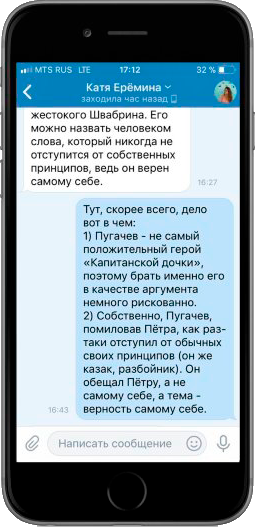
Окружение, в котором невозможно не учиться!
Команда сильных преподавателей и мотивированных учеников формируют особую рабочую атмосферу, которая подвигнет любого выпускника на плодотворную серьезную учебу.
Один из элементов рабочей атмосферы – обязательность выполнения домашнего задания в формате целого полного экзамена. Этот принцип дает возможность проходить материал без пробелов в знаниях.
Результаты учеников на ЕГЭ 2018!
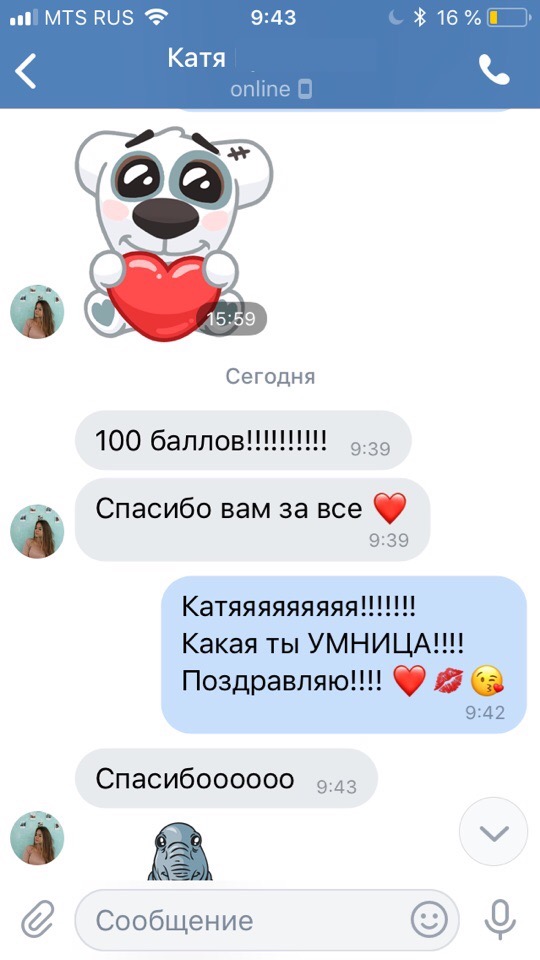
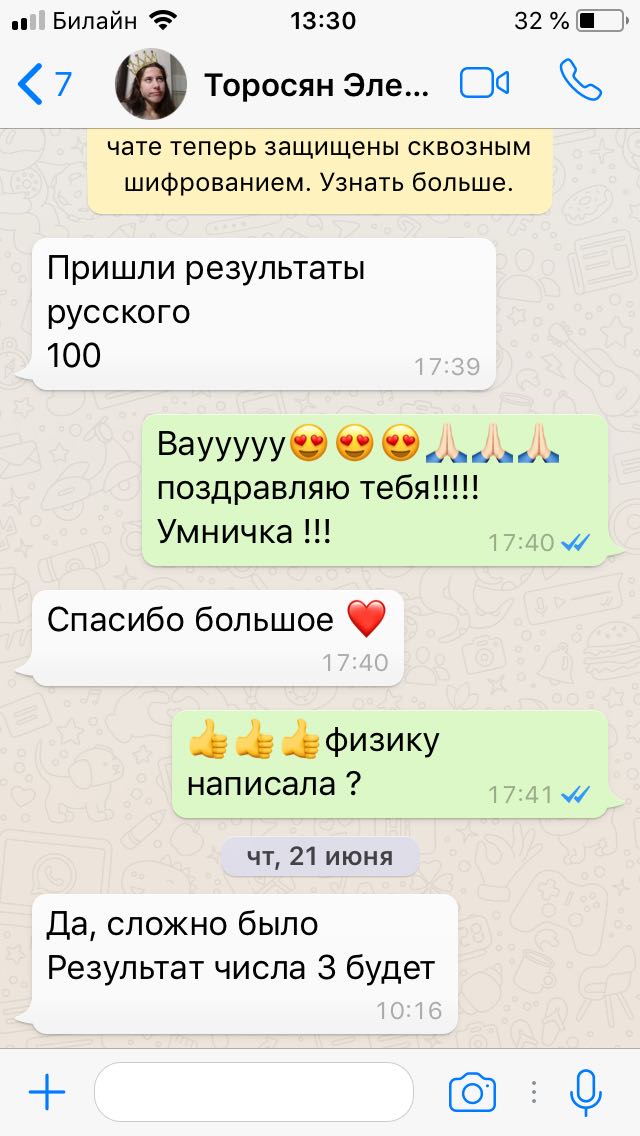
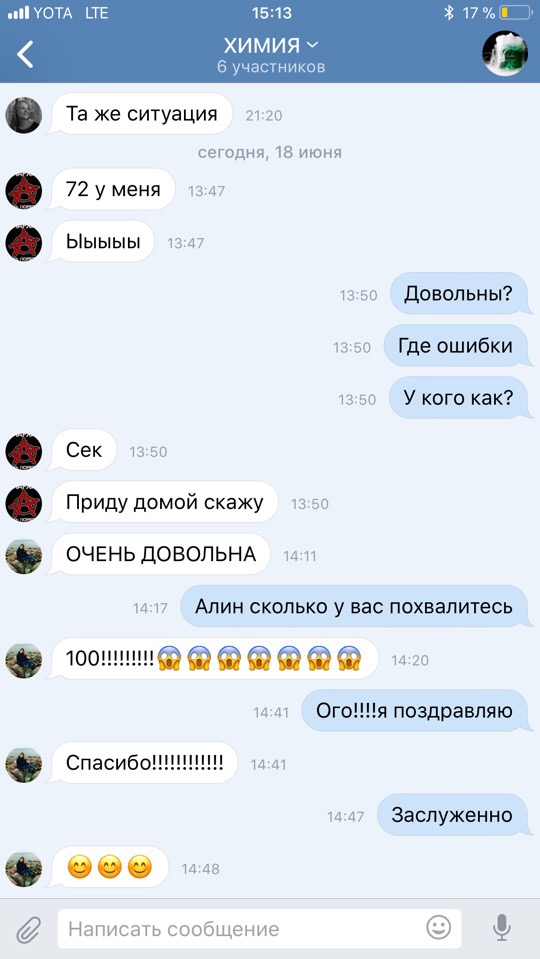
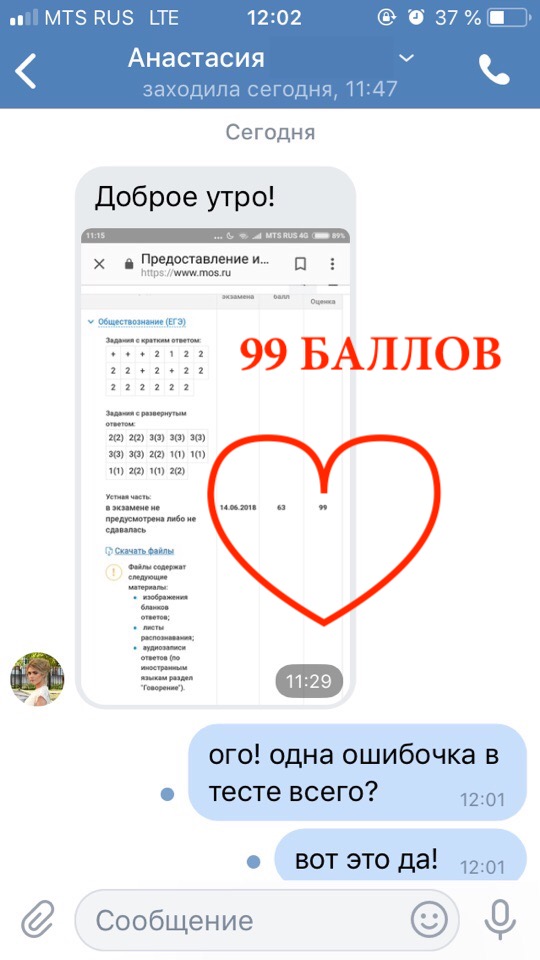
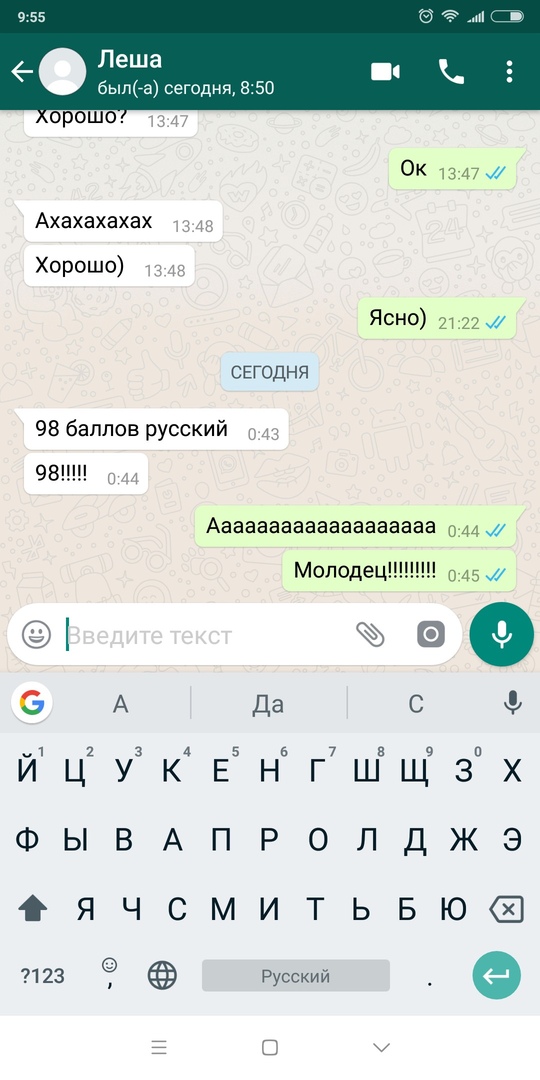
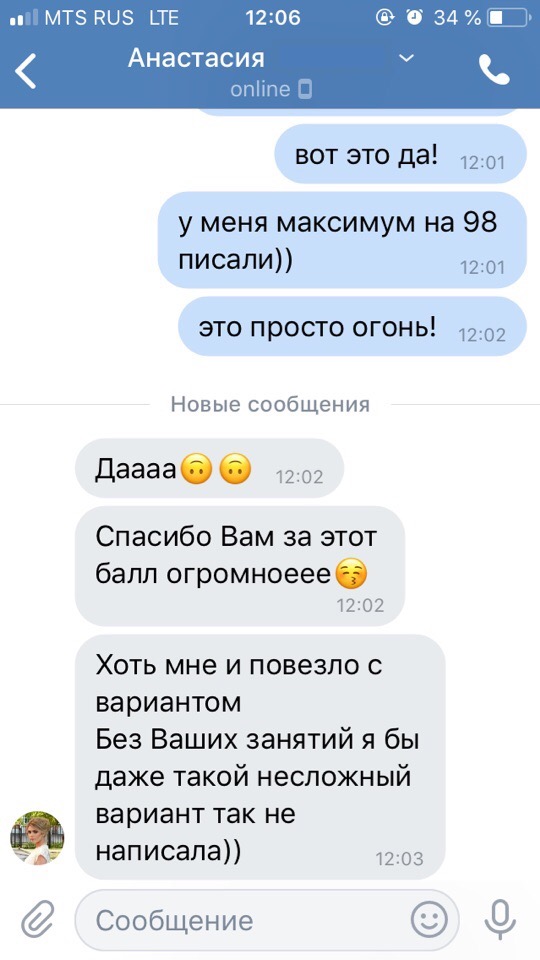
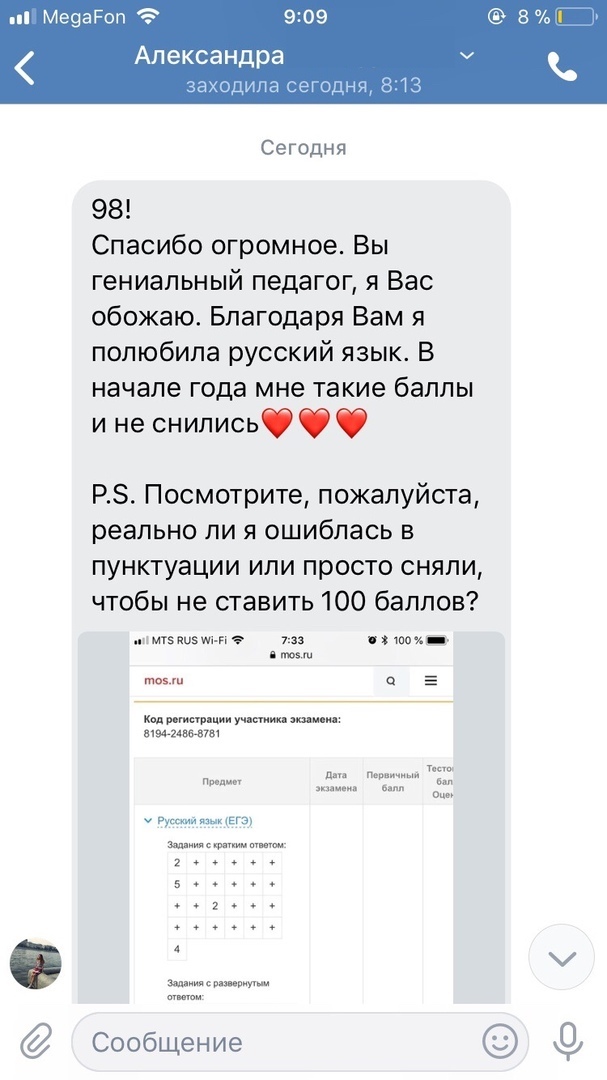
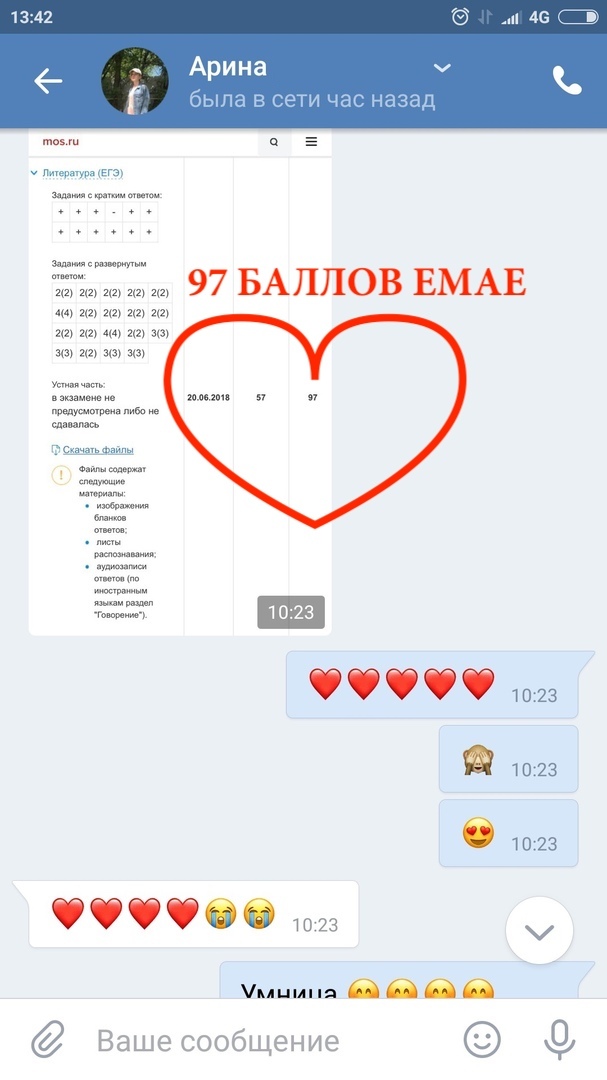
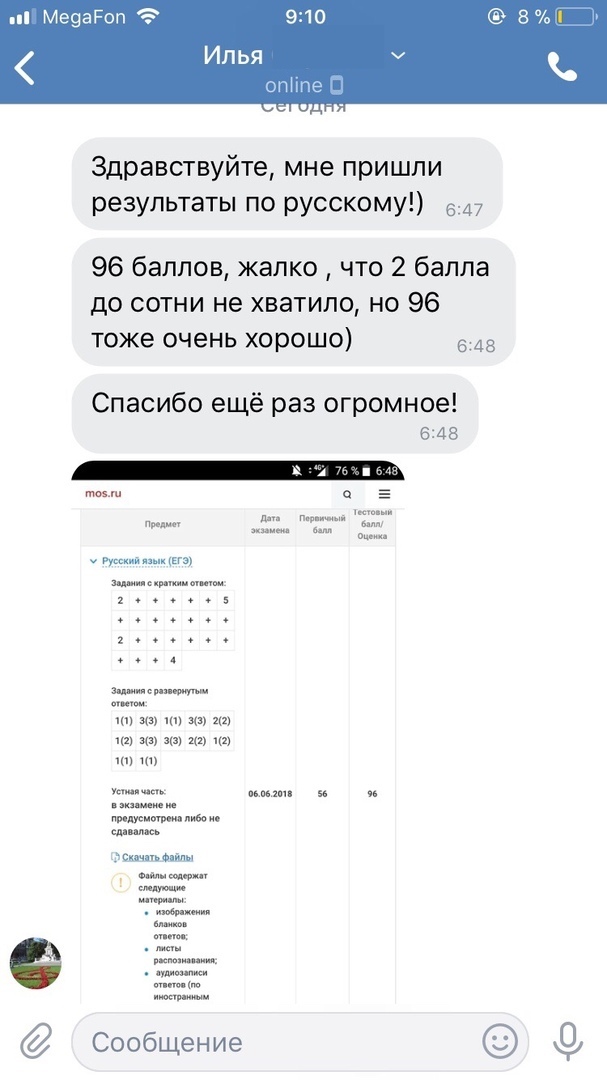
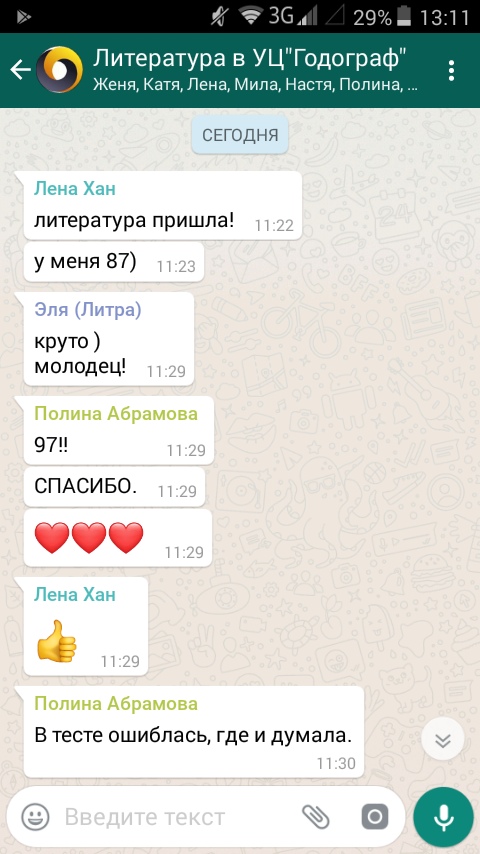
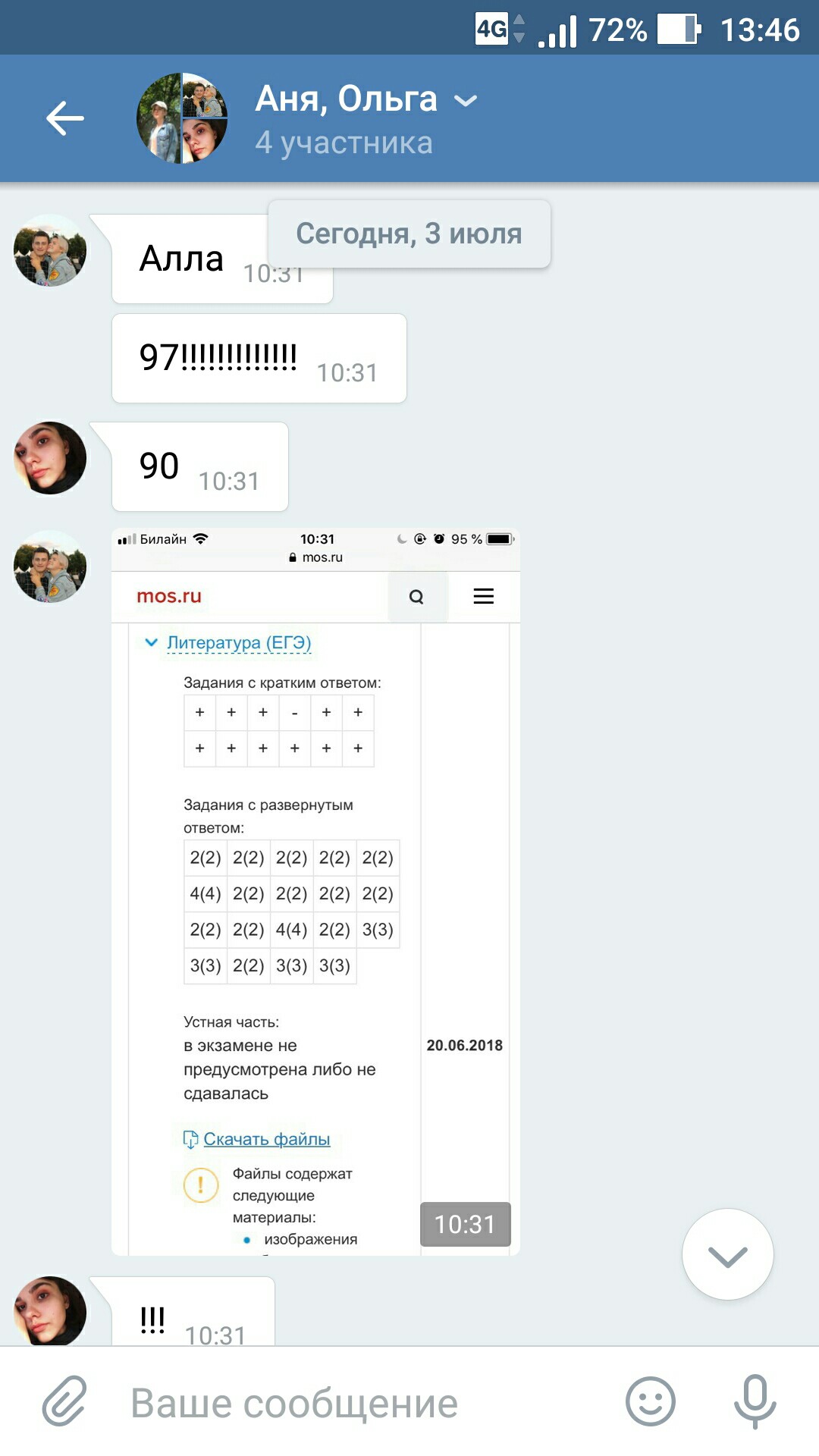
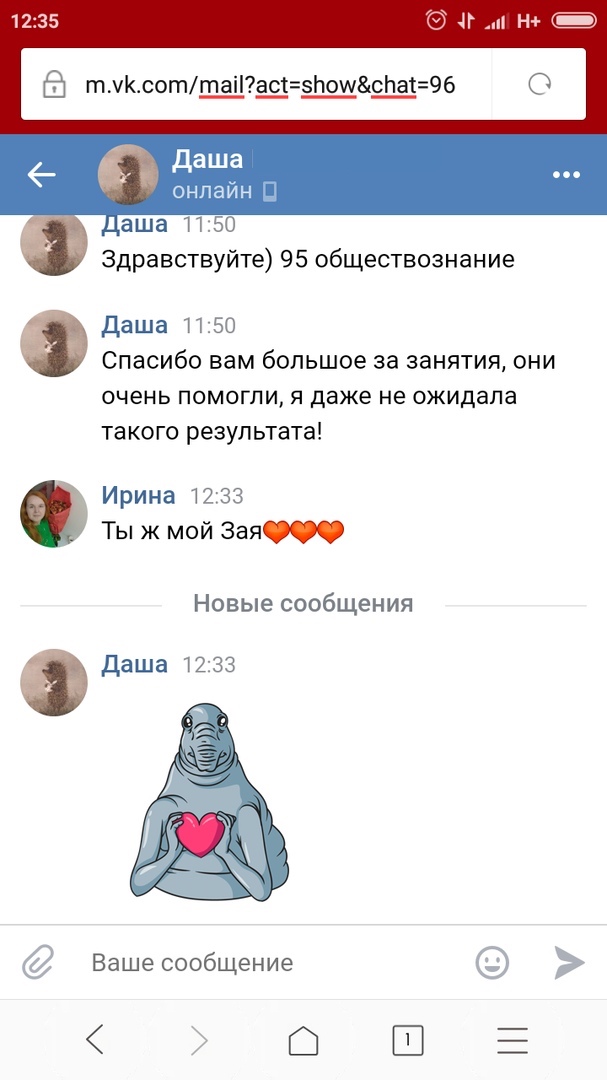
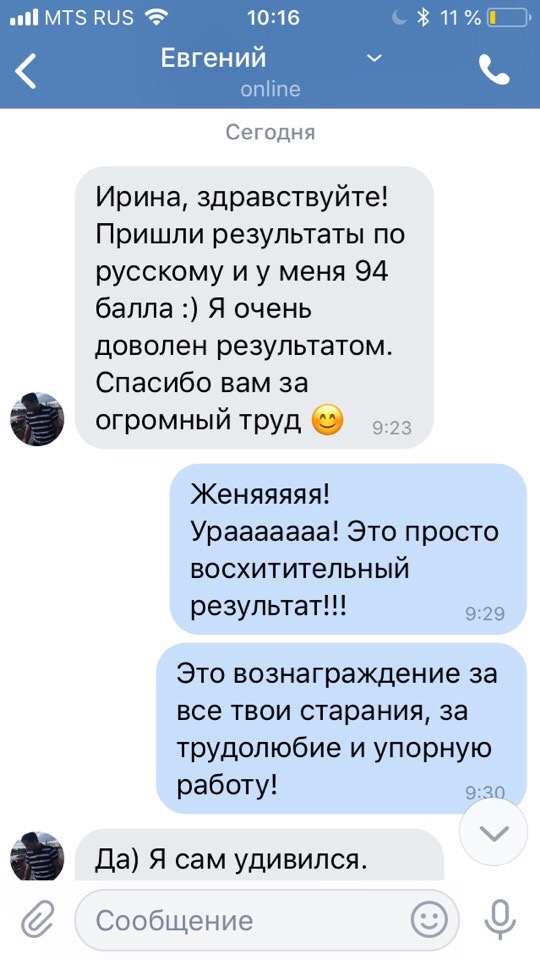
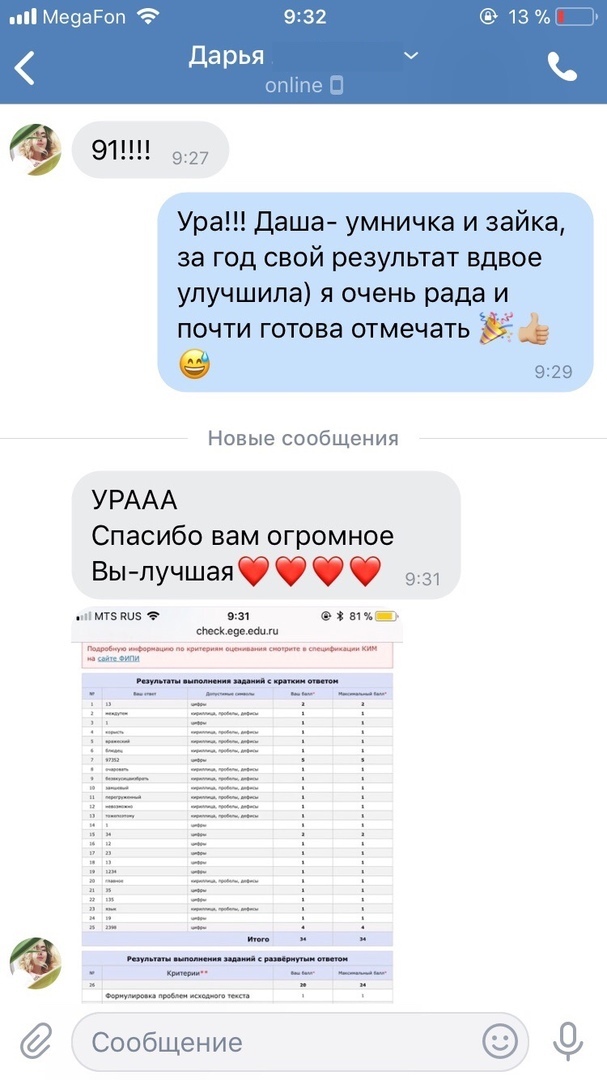
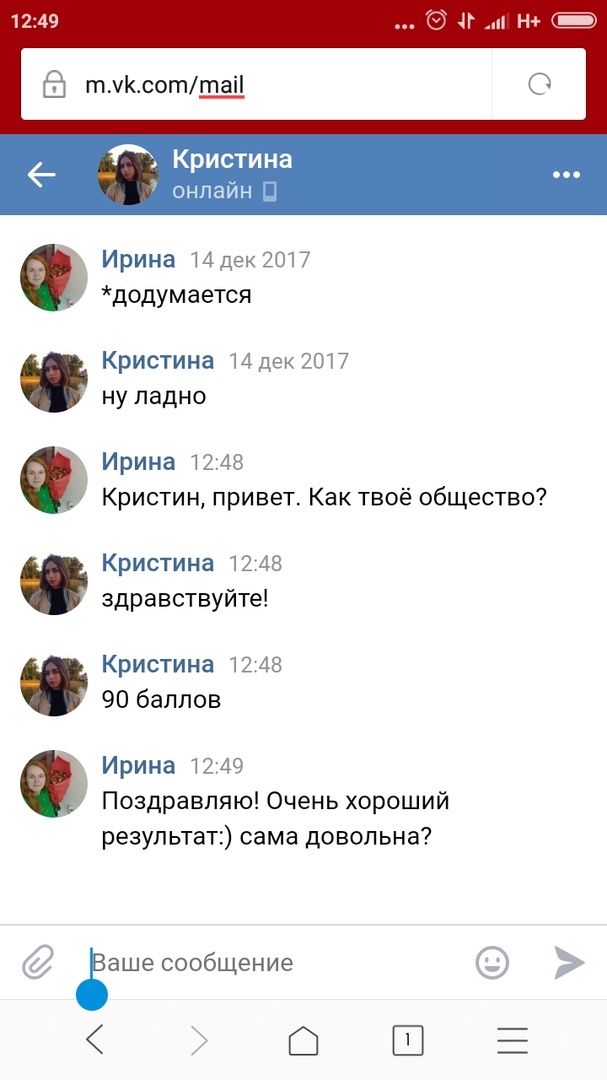
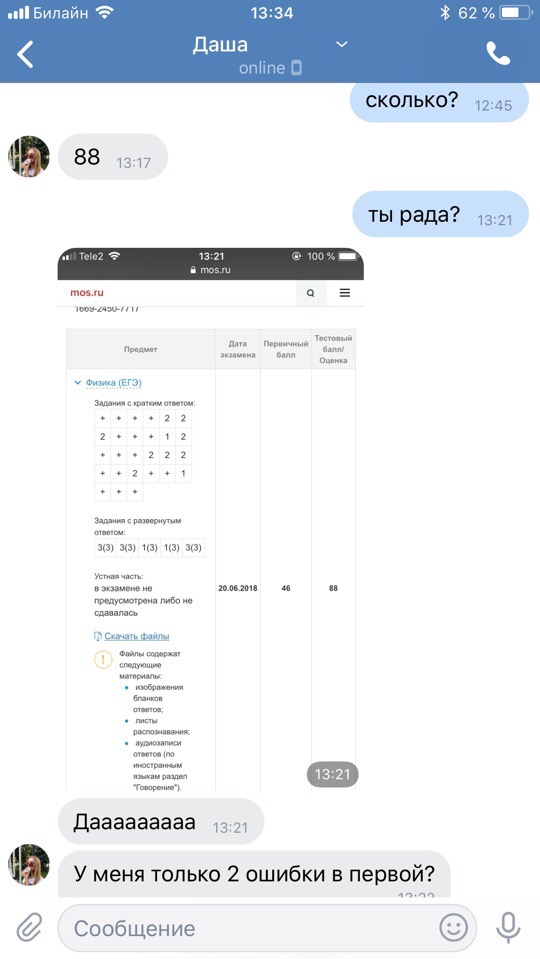
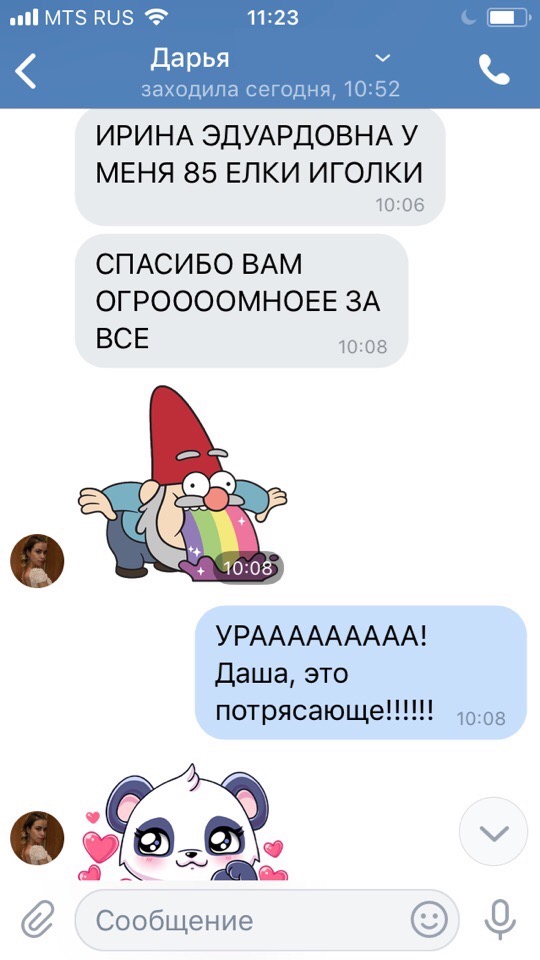
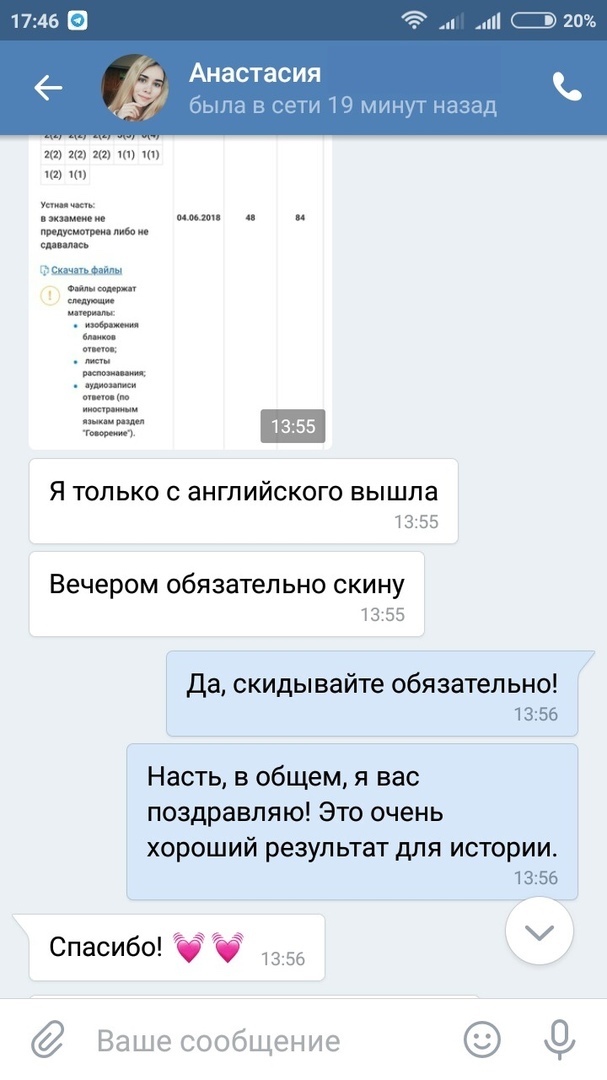
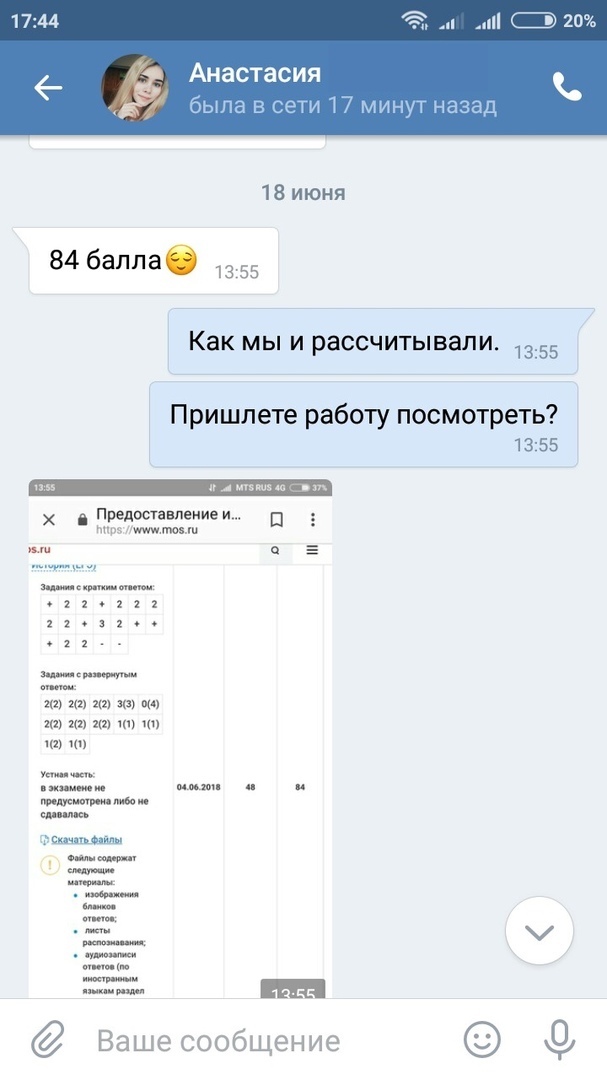
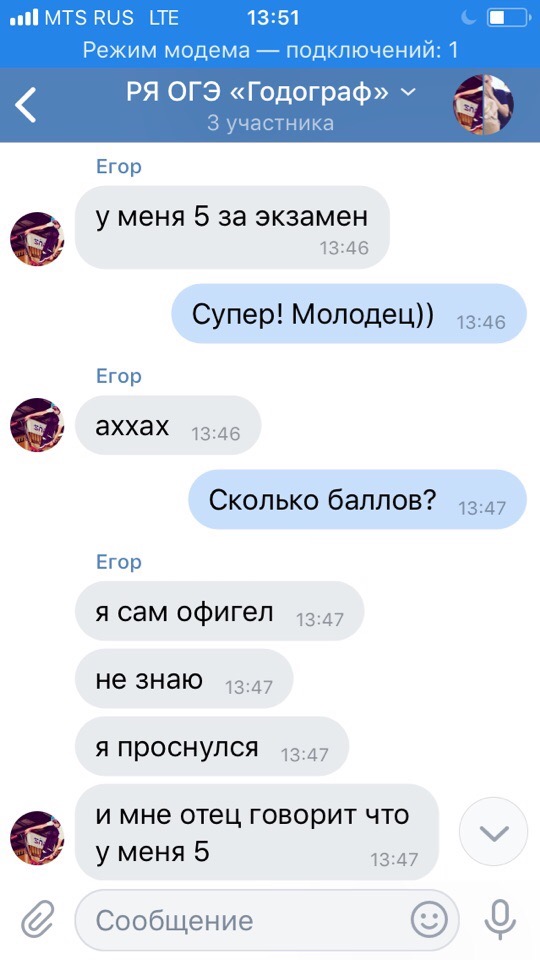
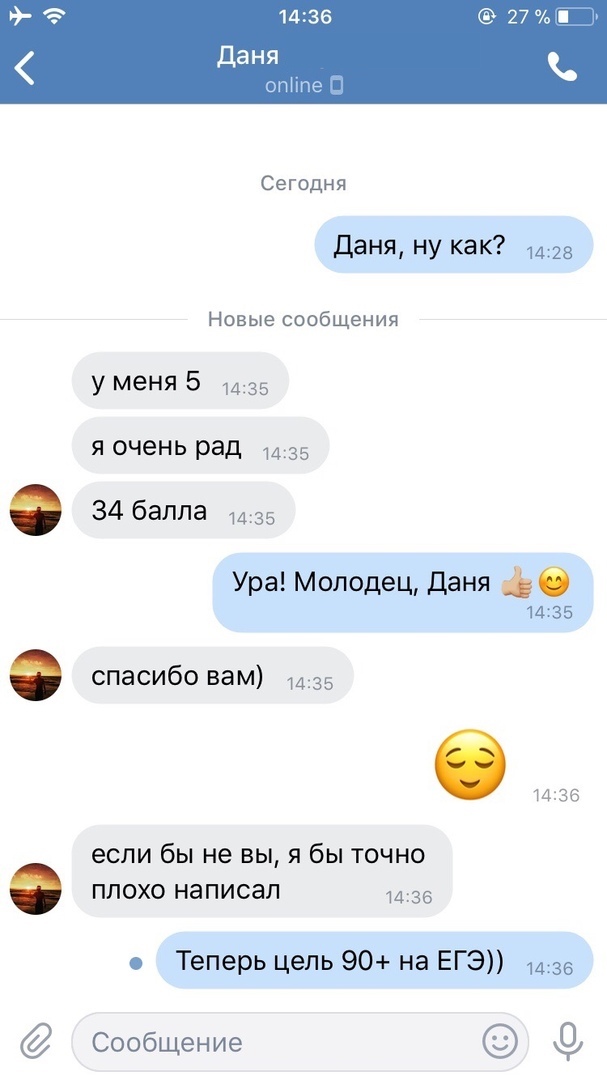
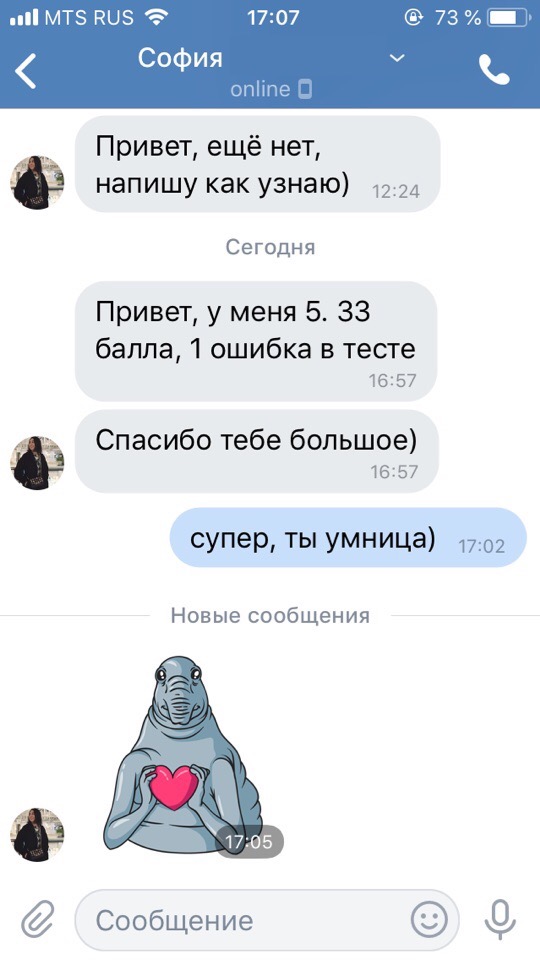
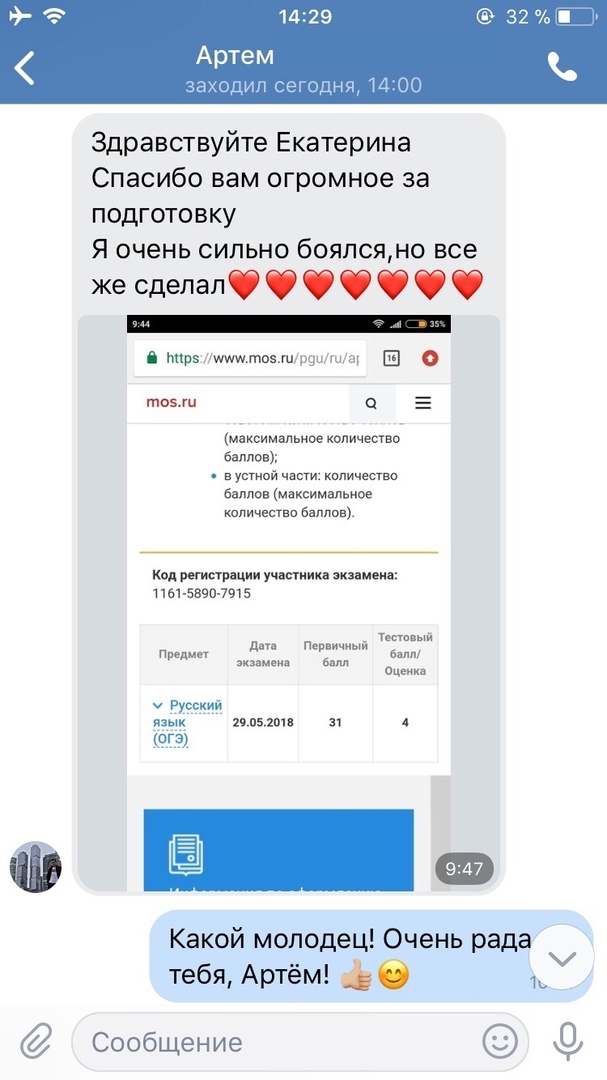
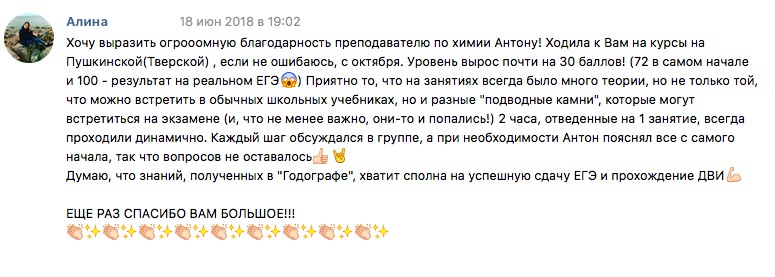
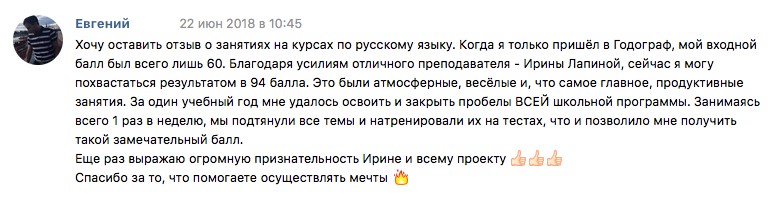


1 занятие в неделю по 120 минут и объемные домашние задания, которые нельзя не выполнять
2-8человек в любой группе нашего центра
120минут длительность одного занятия
79средний итоговый результат учеников центра. На 29 баллов больше, чем по России
+51средний прирост баллов за один курс обучения в центре
Все центры находятся в шаговой доступности от метро (от 3 до 10 минут)
Нажимая на кнопку "Оставить заявку", я даю согласие на обработку персональных данных и соглашаюсь c условиями сайта
Собственная методическая программа на курсах подготовки к ЕГЭ по математике 2019.
Разработана лучшими методистами нашего центра.
За 4 года работы мы выяснили, почему многим ученикам с трудом дается математика. На базе опыта работы со старшеклассниками было создано специальное пособие по подготовке к ЕГЭ по математике, по которому ведутся занятия. Мы ежегодно дорабатываем его, чтобы учесть все тонкости и изменения в стандарте экзамена!
Курс занятий выстроен так, что ученики, повторив материал школьной программы, сразу приступают к решению заданий формата Единого государственного экзамена. Ведь необходимо не только закрыть пробелы в знаниях, но и уметь работать именно по формату Единого государственного экзамена.
План программы ЕГЭ 2019 базового уровня
Программа подготовки по математике для учеников высокого уровня
Автор: Мамин Э.А.
21 занятие по 120 минут (42 часа)
На каждое занятие выделено 3 академических часа. Они могут быть распределены по темам занятия в зависимости от степени усвоения учениками материала.
Освоение минимальных знаний и навыков, необходимых и достаточных для получения балла за ЕГЭ (не ниже 80 по математике профильного уровня), успешные выступления на вузовских олимпиадах Умение рационально распределить время между заданиями, независимо от формата экзамена.
- Системная подача материала по математике в соответствии со школьной программой и материалом, необходимым для решения задач повышенной сложности, встречающихся в олимпиадах.
- Свободное владение методами решения задач всех разделов школьной математики, владение стандартными схемами решения задач. Умение решать одну и ту же задачу несколькими разными способами, с выбором наиболее оптимального.
- Владение арифметикой, а также методами сравнения действительных чисел, подходами, позволяющими проводить сравнение наименее затратным путем. Знание таблицы квадратов наизусть.
- Развитие в учащемся навыка чтения алгебраической записи математического выражения. Понимание алгебраических символов, работа с буквенными выражениями.
- Знание свойств степени, корня, логарифма и умение их применить для преобразования числовых и буквенных выражений. Упрощение алгебраических выражений. Тождественность выражений. Умение анализировать рациональность или нужность того или иного тождественного преобразования применительно к разным задачам. Тригонометрические тождества. Умение записывать буквенное выражение способом, оптимальным для решения задачи, умение проводить преобразование с учетом области определения функций содержащихся в задаче.
- Умение решать линейные, квадратные, рациональные, иррациональные, показательные, логарифмические, тригонометрические уравнения. Уравнения с модулем. Уравнения, содержащие параметр. Понятие равносильности уравнений и действий над уравнениями, ее сохраняющие.
- Умение решать линейные, квадратные, рациональные, иррациональные, показательные, логарифмические, тригонометрические неравенства. Неравенства с модулем. Неравенства, содержащие параметр. Понятие равносильности неравенств и действий над неравенствами, ее сохраняющие.
- Понятие функции, графика функции, способы исследования функций. Умение построить эскиз функции по ее производной.
- Знание свойств плоскости и пространства, необходимых для решения задач планиметрии и стереометрии. Умение доказывать теоремы, леммы и свойства из школьного курса геометрии, достаточные для успешных выступлений на вузовских олимпиадах, владение аксиоматикой геометрии, умение выводить новые утверждения из уже доказанных. Умение доказывать от противного, умение опровергать ложные утверждения контрпримерами. Умение рассмотреть разные возможности ориентирования геометрических объектов.
- Знание теории вероятности применительно к задачам повышенной сложности. Понятие перестановки, сочетания, размещения. Владение методом математической индукции для доказательства свойств и решения задач из теории вероятности, комбинаторики, алгебры.
- Умение самостоятельно проконтролировать правильность решения в тех случаях, когда это возможно, оценить правомерность собственных выкладок, логических переходов.
- Умение проанализировать и оценить свой ответ и свое решение на наличие логически неверных шагов, проанализировать его с точки зрения математической логики, здравого смысла, повседневного опыта.
- Прояснение учащимся методики работы сКИМ, выработка умения правильно читать текст задания, понимать вопросы.
- Заполнение бланков с соблюдением требований.
| Вид деятельности |
| Проверка письменного домашнего задания и тест |
| Повторение прошлого материала |
| Разбор новой темы (теоретический материал и его практика в заданиях 1 части ЕГЭ) |
| Консультативная часть занятия |
Примерный тематический план занятий:
На первом занятии ученики отрабатывают навыки работы с теорий числа в объеме школьного курса, решают задачи, встречающие во второй части ЕГЭ, и олимпиадах. Учатся переводить бесконечную периодичную дробь в десятичную. Изучают основную теорему алгебры, бином Ньютона, треугольник Паскаля. Решают задачи, требующие знания понятий сочетания, размещения, перестановки.прогрессии, метод математической индукции, его применение в решении задач, доказательстве свойств, деление уголком многочлена на многочлен, теорему Безу, иррациональные выражения, избавление от иррациональности в знаменателе. Рассматривают упрощение алгебраических выражений, рациональных и иррациональных. Решают задачи на доказательства тождеств и неравенство Коши.
Решение нестандартных алгебраических уравнений. Выделение полного квадрата. Графические методы. Контроль за стилем ведения записей, в особенности в задачах, требующих объемных выкладок. Совокупность и система уравнений и неравенств. Модуль числа, график функции, решение простейших уравнений, содержащих модуль.
Последовательности. Понятие предела функции, производной. Исследование функций на монотонность, построение графиков функций. Задачи на оптимизацию, на поиск минимума-максимума. Решение иррациональных уравнений, равносильные переходы. Нестандартные уравнения, использование свойств монотонности функций входящих в уравнения. Графические методы.
Показательная функция. Понятие логарифма. Свойства логарифма. Задачи. Логарифмическая функция. Логарифмические уравнения. Задачи. Сравнение действительных чисел, в том числе, сравнение логарифма и степени. Метод разделения выражений для их сравнения. Графические методы сравнения. Равносильные переходы для решения логарифмических и показательных уравнений и неравенств. Комбинированные неравенства. Неравенства, где в ответе есть изолированное решение.
Планиметрия. Аксиоматика. Упор на умение самостоятельно доказывать теоремы и свойства. Доказательство от противного. Опровержение контрпримерами. Теоремы школьного курса. Разные способы расчета площадей. Различные способы ориентации точек и фигур при наложении условий задачи, анализ возможностей существования разных чертежей для одной задачи. Общая культура построения чертежа.
Тригонометрия. Определения синуса и косинуса на тригонометрическом круге. Вывод тригонометрических тождеств. Решение уравнений, отбор корней, принадлежащих заданной области. Графики тригонометрических функций.
Сечение фигуры. Объем. Применение формул. Задачи. Векторы на плоскости и в пространстве. Скалярное произведение векторов. Координатная запись вектора. Уравнение сферы, расстояние между двумя точками с данными координатами. Задачи. Векторные методы решения задач планиметрии и стереометрии. Пояснение доказательства с помощью цветных карандашей. Нормаль к плоскости, уравнение плоскости, прямой. Решение задач.
Решение задач. Материал распределяется по времени с учетом усвоения учениками.
План программы ЕГЭ 2019 продвинутого уровня
Программа подготовки по математике для учеников высокого уровня
Автор: Мамин Э.А.
21 занятие по 120 минут (42 часа)
На каждое занятие выделено 3 академических часа. Они могут быть распределены по темам занятия в зависимости от степени усвоения учениками материала.
Освоение минимальных знаний и навыков, необходимых и достаточных для получения балла за ЕГЭ (не ниже 80 по математике профильного уровня), успешные выступления на вузовских олимпиадах Умение рационально распределить время между заданиями, независимо от формата экзамена.
- Системная подача материала по математике в соответствии со школьной программой и материалом, необходимым для решения задач повышенной сложности, встречающихся в олимпиадах.
- Свободное владение методами решения задач всех разделов школьной математики, владение стандартными схемами решения задач. Умение решать одну и ту же задачу несколькими разными способами, с выбором наиболее оптимального.
- Владение арифметикой, а также методами сравнения действительных чисел, подходами, позволяющими проводить сравнение наименее затратным путем. Знание таблицы квадратов наизусть.
- Развитие в учащемся навыка чтения алгебраической записи математического выражения. Понимание алгебраических символов, работа с буквенными выражениями.
- Знание свойств степени, корня, логарифма и умение их применить для преобразования числовых и буквенных выражений. Упрощение алгебраических выражений. Тождественность выражений. Умение анализировать рациональность или нужность того или иного тождественного преобразования применительно к разным задачам. Тригонометрические тождества. Умение записывать буквенное выражение способом, оптимальным для решения задачи, умение проводить преобразование с учетом области определения функций содержащихся в задаче.
- Умение решать линейные, квадратные, рациональные, иррациональные, показательные, логарифмические, тригонометрические уравнения. Уравнения с модулем. Уравнения, содержащие параметр. Понятие равносильности уравнений и действий над уравнениями, ее сохраняющие.
- Умение решать линейные, квадратные, рациональные, иррациональные, показательные, логарифмические, тригонометрические неравенства. Неравенства с модулем. Неравенства, содержащие параметр. Понятие равносильности неравенств и действий над неравенствами, ее сохраняющие.
- Понятие функции, графика функции, способы исследования функций. Умение построить эскиз функции по ее производной.
- Знание свойств плоскости и пространства, необходимых для решения задач планиметрии и стереометрии. Умение доказывать теоремы, леммы и свойства из школьного курса геометрии, достаточные для успешных выступлений на вузовских олимпиадах, владение аксиоматикой геометрии, умение выводить новые утверждения из уже доказанных. Умение доказывать от противного, умение опровергать ложные утверждения контрпримерами. Умение рассмотреть разные возможности ориентирования геометрических объектов.
- Знание теории вероятности применительно к задачам повышенной сложности. Понятие перестановки, сочетания, размещения. Владение методом математической индукции для доказательства свойств и решения задач из теории вероятности, комбинаторики, алгебры.
- Умение самостоятельно проконтролировать правильность решения в тех случаях, когда это возможно, оценить правомерность собственных выкладок, логических переходов.
- Умение проанализировать и оценить свой ответ и свое решение на наличие логически неверных шагов, проанализировать его с точки зрения математической логики, здравого смысла, повседневного опыта.
- Прояснение учащимся методики работы сКИМ, выработка умения правильно читать текст задания, понимать вопросы.
- Заполнение бланков с соблюдением требований.
| Вид деятельности |
| Проверка письменного домашнего задания и тест |
| Повторение прошлого материала |
| Разбор новой темы (теоретический материал и его практика в заданиях 1 части ЕГЭ) |
| Консультативная часть занятия |
Примерный тематический план занятий:
На первом занятии ученики отрабатывают навыки работы с теорий числа в объеме школьного курса, решают задачи, встречающие во второй части ЕГЭ, и олимпиадах. Учатся переводить бесконечную периодичную дробь в десятичную. Изучают основную теорему алгебры, бином Ньютона, треугольник Паскаля. Решают задачи, требующие знания понятий сочетания, размещения, перестановки.прогрессии, метод математической индукции, его применение в решении задач, доказательстве свойств, деление уголком многочлена на многочлен, теорему Безу, иррациональные выражения, избавление от иррациональности в знаменателе. Рассматривают упрощение алгебраических выражений, рациональных и иррациональных. Решают задачи на доказательства тождеств и неравенство Коши.
Решение нестандартных алгебраических уравнений. Выделение полного квадрата. Графические методы. Контроль за стилем ведения записей, в особенности в задачах, требующих объемных выкладок. Совокупность и система уравнений и неравенств. Модуль числа, график функции, решение простейших уравнений, содержащих модуль.
Последовательности. Понятие предела функции, производной. Исследование функций на монотонность, построение графиков функций. Задачи на оптимизацию, на поиск минимума-максимума. Решение иррациональных уравнений, равносильные переходы. Нестандартные уравнения, использование свойств монотонности функций входящих в уравнения. Графические методы.
Показательная функция. Понятие логарифма. Свойства логарифма. Задачи. Логарифмическая функция. Логарифмические уравнения. Задачи. Сравнение действительных чисел, в том числе, сравнение логарифма и степени. Метод разделения выражений для их сравнения. Графические методы сравнения. Равносильные переходы для решения логарифмических и показательных уравнений и неравенств. Комбинированные неравенства. Неравенства, где в ответе есть изолированное решение.
Планиметрия. Аксиоматика. Упор на умение самостоятельно доказывать теоремы и свойства. Доказательство от противного. Опровержение контрпримерами. Теоремы школьного курса. Разные способы расчета площадей. Различные способы ориентации точек и фигур при наложении условий задачи, анализ возможностей существования разных чертежей для одной задачи. Общая культура построения чертежа.
Тригонометрия. Определения синуса и косинуса на тригонометрическом круге. Вывод тригонометрических тождеств. Решение уравнений, отбор корней, принадлежащих заданной области. Графики тригонометрических функций.
Сечение фигуры. Объем. Применение формул. Задачи. Векторы на плоскости и в пространстве. Скалярное произведение векторов. Координатная запись вектора. Уравнение сферы, расстояние между двумя точками с данными координатами. Задачи. Векторные методы решения задач планиметрии и стереометрии. Пояснение доказательства с помощью цветных карандашей. Нормаль к плоскости, уравнение плоскости, прямой. Решение задач.
Решение задач. Материал распределяется по времени с учетом усвоения учениками.
Группы от 2 до 7 человек. Средний размер группы — 4 ученика
1 х 120 — обычный курс
Курс рассчитан до самого экзамена
Длительность — занятий 3х40 минут = 120 минут
Удобное расписание
Выходные дни и вечера в будние дни
SMS отчетность и анализ успеваемости учеников
+51 баллов за курс подготовки по математике по ЕГЭ
| ПРЕДМЕТ | Баллы по России в 2018 году | Баллы наших учеников до старта курса | Баллы наших учеников на ЕГЭ | Средний прирост баллов за курс обучения | Максимальный балл |
| Математика | 49,8 | 27,45 | 60,9 | 33,45 | 92 |





















































































 Постановка цели на учебный год. Мы не готовим к ЕГЭ, мы готовим к ЕГЭ на определенный балл. Это означает, что план и интенсивность подготовки зависит от ваших целей. Нагрузка в случае, если цель - 70 баллов, сильно отличается от нагрузки в случае, когда цель - 90 баллов.
Постановка цели на учебный год. Мы не готовим к ЕГЭ, мы готовим к ЕГЭ на определенный балл. Это означает, что план и интенсивность подготовки зависит от ваших целей. Нагрузка в случае, если цель - 70 баллов, сильно отличается от нагрузки в случае, когда цель - 90 баллов.

 При работе по данной схеме прогресс будет заметен после каждого урока!
При работе по данной схеме прогресс будет заметен после каждого урока!
